1. はじめに
1-1 感染症と数理モデル
この記事を執筆している2020年3月末現在,新型コロナウイルス感染症(COVID-19)が世界中で猛威を振るっている.日本においても,新規感染者数の増加の傾向が見られており,重大な局面である.
このウィルスは文字通り新型であり,人類がこれまでに直面していないものである.しかし,感染症の発生とその広がりという現象は,普遍的であり人類は何度も経験してきた.例えば,ペストは歴史上何度か大流行が発生し,甚大な被害を引き起こした.特に14世紀の世界的大流行は有名であり,全世界で1億人が死亡したとされている.また,1918年から1920年にかけて流行したスペインかぜは,世界の全人口の1/4が感染したのではないかとされている.このような感染症の発生,流行,収束過程に何らかの法則がないだろうか.
人と人の間のいわゆる「濃厚接触」(以下これを「相互作用」と呼ぶことにする.)で感染症が広がる現象は,一般的に見られる.またこの伝搬現象を数学的に抽象化し,共通の性質を抽出するアプローチが可能である.著名なモデルにKermackとMcKendrickによる,「SIRモデル」と呼ばれる数学的なモデルがある(Kermack and McKendrick 1927).これは微分方程式による,ウイルス流行の数理モデルである.SIRモデルの詳細な解説や文献リストは,資料「この感染は拡大か収束か:再生産数 R の物理的意味と決定」を参照していただきたい.WEB上には他にも多くの解説がある.
1-2 シミュレーション
数理モデルと関係の近い研究手法として,シミュレーションがある.シミュレーションとは,現実に対応する数学的な表現を用いて,コンピュータ内で現実の世界を模擬することにより,解析や予測を行う手法である.SIRモデルもシミュレーションの一種であると捉えることもできる.感染者数などの全体を対象とする量を用いて,その性質を考察する.巨視的でトップダウン的な手法であり,変数が少なく数学的取り扱いが容易である.しかし,その一方として,このアプローチでは,系を構成する個々の要素の詳細な性質を捉えることができない.また、空間的非一様性などを扱うことができないなどの弱点もある.
シミュレーションにはもう一つのアプローチがある.個々の要素の振る舞いを記述し,微視的でボトムアップ的観点で系の性質を調べる手法である.これは計算量が多く、数学的・解析的取り扱いが困難であるなどのデメリットはある.しかしこのようなシミュレーションは、トップダウン的なモデルでは難しいような非一様性や、個々の詳細な振る舞いを記述できる.また、結果が可視化されるため現象の直感的理解がしやすいというメリットもある.
1-3 この解説について
筆者の専門は理論天体物理学・数値シミュレーションであり,疫学や感染症の専門家ではない.しかし,普段研究で使っているシミュレーションで何か知見は得られないだろうかと思い,この記事の執筆を行うことにした.本記事の目的は,ウイルス流行の数学的モデル(SIRモデル)のエッセンスを、個々の人の振る舞いを記述する微視的な数値シミュレーションによって可視化することより,SIRモデルが想定している状況を理解しやすくすることである.今後の新型コロナウイルス感染症(COVID-19)の推移の予測が目的ではないことに留意して頂きたい.
本稿は科学に関心のある高校生や大学生を想定して執筆した.グラフやシミュレーション結果の可視化などを見ながら読み進めて頂ければ,感染症の伝搬という現象を直感的に理解していただけるのではないかと考えている.また,3-2節から3-6節は微分方程式などの大学で学ぶ数学の内容を含んでいる.シミュレーション結果の解析に対する数学的な補足であるため,この部分は飛ばして読んでいただくことも可能である.
2. シミュレーションの方法
2-1 格子型モデル
シミュレーションを行う際に,世界の全てを事細かに再現するモデリングは,コンピュータ資源の問題や,モデルが複雑になりすぎることから現実的ではない.よって,シミュレーションで検討したい内容に応じて現実の抽象化・単純化を行うことになる.
今回は,感染症の伝搬と飽和の過程を検討するのが目的であることから,思い切って単純なモデルを採用する.$100 \times 100$の2次元格子世界を考える.この格子上に排他的に人を配置する(図1).排他的という意味は,1個の格子上の点には一人しか入れないという意味である.
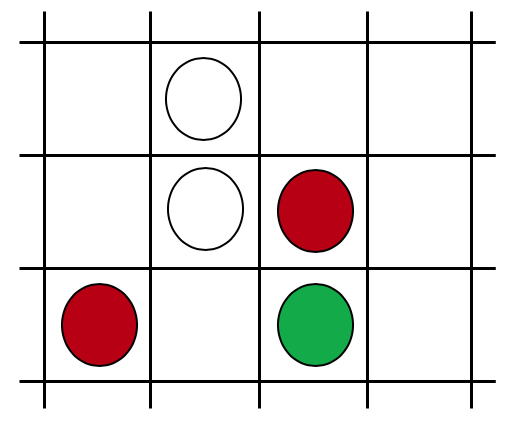
実際の世界では格子上に人が住んでいるわけではない.これはどう解釈すればよいだろうか.この格子を物理的空間と対応させて捉える必要はない.やや抽象的であるが,社会的な位置を示していると考える.隣接する格子間で社会的な繋がりがあるという意味である.例えば,2つの隣接する格子は,家族関係,友人関係,学校・職場の関係などの社会的なつながりを意味すると考える.なので,この格子空間上の離れた2点は,社会的な繋がりの意味で遠いと解釈する.
2-2 境界条件
また,シミュレーションで問題になるのは境界条件である.シミュレーションの世界は,コンピュータの資源の問題で必ず限りがある.その場合,世界の端が生じるのである.扱う問題にもよるが,境界条件の扱いによっては結果が大きく変わることもありうる.今回は周期境界条件を採用した.これは左端と右端,または上端と下端の境界が繋がっているという取り扱いである(図2).この境界条件では,境界の点が特別な点ではなくなるため,今回のシミュレーションには適していると考えられる.

2-3 感染症伝搬のモデリング
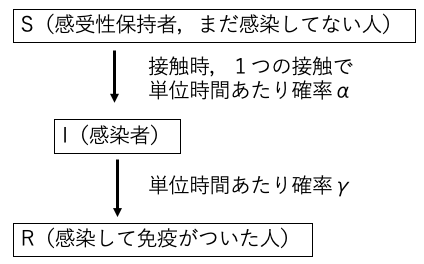
格子状の隣合う人と人との間で相互作用をして,系全体が時間発展する.SIRモデルのコンセプトに従い,人はそれぞれ3つの内部状態を持っているとする(図3).
- 感受性保持者(Susceptible).まだ感染していない人.
- 感染者(Infected)
- 免疫保持者(回復者)(Recovered).感染を経験した後に治癒し,免疫を獲得した人.
感受性保持者(以下$S$と呼ぶ)は,感染者(以下$I$と呼ぶ)と接触すると,感染するリスクに晒される.このモデルでは格子上の周囲の8点にいる人と接触していると仮定する.接触の結果,必ず感染するわけではない.このモデルでは,感染するかどうかは確率的であると仮定する.単位時間あたり一人の感染者から感染する確率を$\alpha$とおく.よって,周囲に複数の感染者がいる場合は,$\alpha$にその人数を乗じた確率であると仮定できる.たとえば周囲に感染者が3人の場合は,単位時間あたりに$3 \alpha$の確率で感染する.
ここで単位時間あたりの確率という言葉を用いた.単位時間とは1秒や1日など基準となる時間のことである.例えば時間単位が1日であれば,1日経過するときの感染確率が$\alpha$であるという意味である.
また,今のシミュレーションの場合の単位時間は,シミュレーションが1ステップ進んだときの時間の経過量である.物理的な時間との対応は特に定めておらず何でも良い.イメージが湧きにくい場合は,このシミュレーションの単位時間は1日とみなしても構わない.その場合は,以下の「単位時間あたり」は「1日あたり」と読み替えれば良い.また,グラフの横軸で時間(Time)を取る場合は,その単位は日である.
感染後は時間が経つと回復する.つまり,感染者$I$から免疫保持者(以下$R$と呼ぶ)に変化する.この回復するかどうかも確率的であるとする.単位時間の間に回復する確率を$\gamma$とおく.
一旦,免疫保持者$R$になった場合,再感染したり,他を感染させることはないとする.なお,現実の新型コロナウイルス感染症(COVID-19)はこのことは明らかではなく,注意が必要である.
2-4 パラメータの物理的意味
以下,物理に馴染みがある方向けの補足である.$\alpha$は単位時間あたりの遷移確率であるため,次元としては時間の逆数の次元を持っている.つまり,$1/\alpha$は時間の次元であるが,これは1対1の接触をどぐれぐらいの時間継続すれば感染するか,その時間尺度に大雑把には対応する.たとえば$\alpha=0.1$というモデルの場合,逆数である時間$10$程度で感染すると考えられる.$\gamma$も同様であり,$1/\gamma$が典型的な治癒するまでの時間尺度である.たとえば$\gamma=0.1$というモデルの場合,逆数である時間$10$程度で回復すると考えられる.このような見積もりを次元解析という.
シミュレーションを行う際にこれらのような典型的時間尺度を把握しておくことが,結果の解釈に重要である.
2-5 初期条件
初期状態は,ほとんどが感受性保持者$S$であるが,一定数の感染者$I$が初期状態においてランダムに発生したとして,その後の感染の広がりを調べる.初期感染者の割合を$n_\mathrm{ini}$とする.例えば,$n_\mathrm{ini}=0.01$の場合は,初期状態で1%の人が感染している状況である.
2-6 シミュレーションパラメータまとめ
今回行ったシミュレーションのパラメータは以下の表1にまとめた.
| モデル名 | $\alpha$
(感染確率) |
$\gamma$
(回復確率) |
$\delta$
(移動確率) |
$n_\mathrm{ini}$
(初期感染者割合) |
$n_\mathrm{void}$
(空隙割合) |
$R_0$
(基本再生算数) |
|---|---|---|---|---|---|---|
| Model 1 感染率:高 |
0.1 | 0.1 | 0 | 0.01 | 0.0 | 4.8 |
| Model 2 感染率:中 |
0.05 | 0.1 | 0 | 0.01 | 0.0 | 2.4 |
| Model 3 感染率:低 |
0.025 | 0.1 | 0 | 0.01 | 0.0 | 1.2 |
| Model 4 接触数:低 |
0.1 | 0.1 | 0 | 0.01 | 0.5 | 1.6 |
| Model 5 移動:あり |
0.1 | 0.1 | 0.2 | 0.01 | 0.5 | 2.3 |
$\delta$と$n_\mathrm{void}$は,後の章で導入するパラメータである.
3. シミュレーションとSIRモデルの比較
3-1 シミュレーション結果
まずは典型的なシミュレーション結果を図4に示す.Model 1[感染率:高]と呼ぶ.感染確率$\alpha=0.1$, 回復確率$\gamma=0.1$, 移動確率$\delta=0$である.

初期感染者はわずか1%であるが,最終的には免疫保持者で埋め尽くされるため,最終的にはほとんどの人が感染経験をしたことに相当する.感染者から周囲に新たな感染者を広げる連鎖が続いていることがわかる.
全体の人数に対するに対する$S$(感受性保持者, 黒の線), $I$(感染者, 赤の線), $R$(免疫保持者, 緑の線)の人数の割合をプロットしたのが以下の図5に示すグラフである.
時間30経過すると系内の90%が感染を経験する.時間125で感染者数0で収束する.最終的に99.8%が感染を経験した.感受性保持者のままで最後まで維持できたのは,0.2%にすぎない.
爆発的な感染の発生の原因は,SIRモデルに戻って考えると理解しやすい.次の節でSIRモデルとの対応を考える.
3-2 SIRモデルのパラメータとの対応関係
この章の以下の節(3-2から3-6)は,SIRモデルとの対応に関する数学的な補足である.数学的な議論が不要な場合は,この章を飛ばして次の章(4章)に進むことも可能である.
本記事の目的は,微分方程式であるSIRモデルをシミュレーションによりその意味を理解することであった.このシミュレーションモデルはSIRモデルに対応するものであろうか.SIRモデルの式を検討しながら考察してみよう.
SIRモデルは以下の連立微分方程式で与えられる.$S$(感受性保持者), $I$(感染者), $R$(免疫保持者)の人数の時間発展方程式は,
$$ \frac{d S}{d t} = – \beta S I$$
$$\frac{d I}{d t} = \beta S I -\gamma I $$
$$\frac{d R}{d t} = \gamma I $$
である.$S+I+R$は対象とする系の総人口であるから保存則が成立する.つまり,実質的には2変数の微分方程式となっている.以下では$R$の方程式は自明であるため扱わない.$\gamma$は,ある感染者に着目したときの単位時間あたりの回復確率であり,シミュレーションの$\gamma$と同じ意味である.次元は時間の逆数である.$\beta$は,シミュレーションと直接対応していないパラメータである.感染者数の増加の比例定数であり,次元が$人^{-1} T^{-1}$である.これらの詳細な解説は,文献「この感染は拡大か収束か:再生産数 R の物理的意味と決定」にある.
シミュレーションでは1対1の相互作用による単位時間あたりの感染確率を$\alpha$としている.モデルの$\beta$も感染しやすさに対応する量であるため,$\alpha$と$\beta$の間に関係があると考えられる.
そのため,以下のような考察をしよう.接触数 $n_\mathrm{n}$ (n neighbour)をある一人を観測したときに,周囲の相互作用可能な人数とする.格子モデルの場合は,周囲の格子は8点であるため,接触数$n_\mathrm{n}$は$0$から$8$の間となる量である.後の章で見るように格子空隙がある場合や,周囲を免疫保持者で囲まれた場合は,8よりも実質的に小さい値になる可能性がある.ここでは調整可能なパラメータとした.
もし,空間的な一様性が仮定できるならば,ある一人を抽出したときに,その人が感染している確率は$I/N_\mathrm{total}$とおけるだろう.ここで$N_\mathrm{total}$は系内の全人数である.実際のシミュレーションにおいては,厳密には正しいとは限らないが,検討の第一歩としてこの仮定をおいた.例えば感染者が空間的に群をなし不均一が生じるような状況下ではこの仮定は誤りだろう.
周囲の感染者の平均的な人数は,
$$周囲の相互作用可能な人数 \times 感染者である確率 = \frac{n_\mathrm{n} I}{N_\mathrm{total}}$$
とおける.
単位時間あたり1対1の相互作用の結果で感染する確率が$\alpha$であるから,周囲の感染者の平均的な人数を考慮すると,単位時間あたりの感染確率は,
$$単位時間あたりの感染確率 = \frac{\alpha n_\mathrm{n} I}{N_\mathrm{total}}$$
とかける.
よって,$S$(感受性保持者)のうち単位時間あたり$\alpha n_\mathrm{n} I/N_\mathrm{total}$の割合で感染者が増加する.一方で,$I$は回復によって単位時間あたり$\gamma$の割合で減少するから,$I$の時間変化の方程式は以下のようにかける.
$$ \frac{dI}{dt} = \frac{\alpha n_\mathrm{n}} {N_\mathrm{total}} IS – \gamma I$$
元のSIRモデルと比較することによって,
$$\beta = \alpha \times \frac{n_\mathrm{n}}{N_\mathrm{total}} $$
となる.シミュレーションパラメータ$\alpha$とモデルパラメータ$\beta$の近似的関係式を得た.
3-3 規格化されたSIRモデル
元のSIRモデルの変数$S$, $I$, $R$はそれぞれの状態(感受性保持者, 感染者, 免疫保持者)の人数である.より解析をしやすくするために,今回は,系の全人口($N_\mathrm{total} = S + I + R$)に対する割合を議論する.それぞれの全人口に対する割合を$s=S/N_\mathrm{total} , i = I/N_\mathrm{total} $として定義して,以下のように変換を行う.
$$ \frac{d s}{d t} = – \alpha n_\mathrm{n} s i$$
$$\frac{d i}{d t} = \alpha n_\mathrm{n} s i -\gamma i $$
この方程式は,$N_\mathrm{total}$に依存しない形でかけている.よって,パラメータ$\beta$ではなくて$\alpha$を用いて,全人口に対する割合で議論すれば,全人口によらない性質を調べることができる.
以上よりシミュレーションと比較可能な方程式を得た.パラメータを取り替えて,シミュレーションと比較できるようにしただけであるため,本質的には元のSIRモデルと違いはない.
3-4 SIRモデルとシミュレーションの比較
この微分方程式を4次Runge-Kutta法を用いて数値的に解いた.結果は以下の図6に示す通りである.Model 1[感染率:高]のシミュレーション結果と合わせて表示してある.$\alpha$, $\gamma$はシミュレーションと規格化されたSIRモデルどちらも同じ値であり,感染確率$\alpha=0.1$, 回復確率$\gamma=0.1$である.$n_\mathrm{n}$はシミュレーションにはないモデルパラメータである.周囲の人数なので$8$ぐらいが想定されるが今回のシミュレーションでは,$4.8$が当てはまりがよかった.本来は,$n_\mathrm{n}$も定数ではない扱いにすべきであるが,Model 1[感染率:高]の場合では,全体の振る舞いとしては,定数としても大きくは違わないようである.
以上より,このシミュレーションはSIRモデルのエッセンスを概ね捉えることができたと考えてよいだろう.
ただし,モデルとの対応の導出の時に,いくつかの近似を用いているので,当てはまりの悪いケースもありうる.Model 2[感染率:中]やModel 3[感染率:低]では傾向はシミュレーションとSIRモデルで似ているものの,定量的なあてはまりはよくなかった.例えば図7に示すようにModel 2[感染率:中]では,SIRモデルとシミュレーションとの間で差異が見られる.$n_\mathrm{n}$の時間変化を考慮するモデルに改良すると,誤差を小さくできるのかもしれない.
3-5 パラメータβの意味
シミュレーションとの比較のために$\beta$を
$$\beta = \alpha \times \frac{n_\mathrm{n}}{N_\mathrm{total}} $$
と表し,$\alpha$と$n_\mathrm{n}/N_\mathrm{total}$の積の形に分解された.これは,社会構造要因とそうでない部分に分けたことに相当する.つまり,$\beta$を下げるには2つのアプローチがあることを意味する.
前者の$\alpha$は1対1相互作用での単位時間あたりの感染確率である.つまり社会的な繋がり数といった社会的構造とは無関係な量である.$\alpha$の値そのものは,ウィルスの性質,感染しやすさなどが反映されている.しかし,これは人間がコントロールできない量であることを意味しない.なぜなら,その社会の平均的な習慣などにも関係していると考えられるからである.たとえば,衛生に関する意識が強く消毒や手洗いなどを意識的にすれば$\alpha$を下げることができる.
後者の$n_\mathrm{n}/N_\mathrm{total}$は社会的な繋がりを表し,ウィルス自体の性質による感染しやすさなどとは無関係な量である.こちらは社会構造に関係しており,意識的に接触を避ければ下げることができるだろう.
3-6 再生産数
SIRモデルでは,$R_0= N_\mathrm{total} \beta/\gamma$を基本再生産数,$R = S \beta/\gamma$を実効再生産数と呼んでいる.これらの再生産数については,文献「この感染は拡大か収束か:再生産数 R の物理的意味と決定」に詳細な議論があるので,ここでは簡単に触れるだけに留める.
今回のモデルでは基本再生産数, 実効再生産数は以下のように表される.
$$ R_0 = \frac{\alpha n_\mathrm{n}}{\gamma},\,\,\, R = \frac{\alpha n_\mathrm{n} s}{\gamma} $$
ここで,$s$は感受性保持者の全体に対する割合である.Model 1[感染率:高] では$\alpha=0.1$, $\gamma=0.1$, $n_\mathrm{n}=4.8$となり,$R_0 \simeq 4.8$と1を大きく超えていたため,感染力が極めて強い状況を考えていた,と言えるだろう.
4. シミュレーションによる解析
4-1 シミュレーションの意義
ここまでで,数理モデル(SIRモデル)の結果の傾向を概ね再現するシミュレーションモデルを構築できることを見た.しかし,SIRモデルを再現するだけでは本質的に何も新しくない.計算に要する時間もSIRモデルの方が圧倒的に短い.では,わざわざシミュレーションする理由は何だろうか.シミュレーションは数理モデルに比べて,より現実に近いモデルへの拡張が比較的容易であるという利点がある.特に空間的な非一様性に関する過程は系全体を数個の変数で表す数理モデルは容易ではないだろう.
この章では,より複雑なモデルでシミュレーションによる考察を続ける.
前の章にも見たように感染者が急増しないために必要なのは,感染者増加の係数である$\beta$を下げることである.$\beta$は,感染確率$\alpha$と社会的な繋がり数$n_\mathrm{n}$に分解できた.これらが変化した場合についてシミュレーションで考察してみよう.
4-2 感染確率が下げられた場合
1対1相互作用による単位時間感染確率$\alpha$は前の章でも述べたように,消毒や手洗いなど衛生に対する意識を徹底することにより下げることができる.$\alpha$が下げられたとした場合のシミュレーションをみてみよう.
$\alpha=0.025$のケース(Model 3[感染率:低])を考える.感染確率が1/4に減った場合である.結果を図8に示す.Model 1[感染率:高]と比べて結果は大きく異なるものとなった.感染症が全体に広がらず,散発的な感染群の発生に留められている.

図9は感染者数の時間変化をグラフにしたものである.最終的な感染経験者が大幅に抑えられている.この実行例では時刻320で収束し,最終的に18.8%が感染を経験した.つまり,感受性保持者$S$のままで最後まで維持できたのは,81.2%となる.
指数関数的に推移する現象であるため,ちょっとしたパラメータの違いが大きな影響を及ぼすのである.感染確率に対する依存性を図10にまとめた.$\alpha=0.1, 0.05, 0.025$の場合のシミュレーション結果の感受性保持者($S$)の時間推移を比較したものである.感染確率を下げると最終的な感染者数に大きな違いが出ることがわかる.
基本再生産数は繋がりの数$n_\mathrm{n}$に依存している.
$$ R_0 = \frac{\alpha n_\mathrm{n}}{\gamma}$$
Model 1[感染率:高]では$n_\mathrm{n} = 4.8$があてはまりがよかった.そこで,この数値で$R_0$を求めるとModel 1[感染率:高]($\alpha = 0.1$)は$R_0 = 4.8$, Model 2[感染率:中]($\alpha = 0.05$)は$R_0 = 2.4$, Model 3[感染率:低]($\alpha = 0.025$)は$R_0 = 1.2$である.基本再生産数$R_0$を減少させて1に近づけるにつれて,感染拡大が抑えられることがわかる.なお,厳密には$n_\mathrm{n}$はModelにも依存し時間変化する量であるので,ここでの見積もりは目安の値である.
4-3 格子空隙の存在
これまでのシミュレーションは格子が完全に埋め尽くされたケースでの考察をした.今度は,格子に空隙がある場合を考えてみる.つまり,人によって,周囲の結合度が違うようなケースに相当し,完全に埋め尽くされている場合に比べて社会的な繋がりのある数を減らした場合に相当する.変更するシミュレーションパラメータは$n_\mathrm{void}$であり,全体に対する空隙率である.
Model 4[接触数:低]は空隙率は$n_\mathrm{void}=0.5$とした.Model 1[感染率:高]と空隙率以外のパラメータは同じである.図11が結果である.

シミュレーション結果を見るとわかるように,Model 1[感染率:高](図4)と比較して,大幅に感染拡大が抑えられている.定量的に確かめるために,感受性保持者($S$)を図12にプロットした.すなわち感染を経験しなかった割合である.空隙を導入することにより感染を避けられた人が大幅に増えている.収束時の$S$(感受性保持者,すなわち感染しなかった人)は空隙がない場合は,0.2%であったのに対して,空隙ありの場合は,77.7%になった.
これは以下のように理解できる.感染者の増加率は
$$\alpha \times n_\mathrm{n}$$
の積に比例する.$\alpha $は1対1での単位時間あたりの感染確率であり,Model 1[感染率:高]とModel 4[接触数:低]どちらも同じ値である.Model 4[接触数:低]で空隙が導入されたことにより$n_\mathrm{n}$が実質的に低下し,そのことにより感染者増加に歯止めがかかったのである.
4-4 人の活動性の影響
空隙がある程度存在するが,人の活動がある場合を考えてみる.人は移動や活動内容により接触する相手が時々刻々と変化するものである.そのことを表現するために,人が格子上を移動することにした.時刻によっては移動しない場合もあり,それは確率的であるとする.単位時間あたりの移動確率を$\delta$とする.移動するときは,周囲の8セルの中で空いたスペースの中の1つをランダムに選んで移動する.空いたスペースがない場合は移動しないとする.
Model 5[移動:あり]はModel 1[感染率:高]やModel 4[接触数:低]と同じ感染確率$\alpha$, 同じ回復確率$\gamma$とした.空隙率は$n_\mathrm{void}=0.5$であり,Model 4[接触数:低]と同じである.単位時間あたりの移動確率は$\delta=0.2$とおいた.結果は以下の図13の通りである.Model 4[接触数:低]と比べて,明らかに感染者の広がりが大きい.

図14に$S$(感受性保持者,すなわち感染しなかった人)をプロットした.人をランダムに移動させた場合は,感染拡大を引き起こしており,収束時の$S$は,77.7%から,18.6%へと大幅に低下した
空隙があることにより時々刻々の人々の周囲の人数は少なくなるが,移動することにより人々の関係のつなぎ変えが頻繁に起きるため,実質的な結合数が増加する.このことにより,大きな感染拡大を引き起こしたと考えられる.
5. まとめ
本記事では,SIRモデルに対応する,単純な格子シミュレーションモデルを構築してみた.概ね妥当と考えられるパラメータによって,シミュレーションより,SIRモデルの結果を再現することができた.
シミュレーションというと複雑なモデルを用いて現実をコンピュータ内に再現し,高精度な予測を行うものと考える方もいるかもしれない.しかし,今回のシミュレーションのモデルは極めて単純化されたものである.容易により複雑なモデルへと拡張できる.しかし,シミュレーション研究はそういった複雑ものばかりでなく,今回のように単純化したモデルもしばしば用いられる.単純化されたモデルを用いることにより重要な点が何かを明らかにすることができるのである.
「はじめに」でも触れたが,本記事は、今後の新型コロナウイルス感染症の詳細な推移の予測が目的ではない.感染症の伝搬の様子を可視化し、それを理解するというのが目的である.
パラメータや設定のわずかな差が、系全体の状態の違いとして返ってくることが理解できたのはないかと思う.これらのパラメータの変化に対応するのは,我々の「行動変容」である.
最後にシミュレーションから得られる知見をまとめる.
(1) 「感染確率の影響」の可視化
シミュレーションのパラメータは,1対1の単位時間あたりの感染確率$\alpha$と、回復までの確率$\gamma$であった.本記事では、$\alpha$を下げることで大規模感染を避ける効果を可視化した.結果は,$\alpha$に敏感である.$\alpha$は1対1接触における単位時間感染確率であることから,手洗いや消毒の励行,マスクの着用,不用意に汚染箇所を触らない、いわゆる「三密(密閉・密集・密接)を避ける」等々様々な工夫で、感染確率$\alpha$を下げることができるだろう.
(2) 「接触数の影響」の可視化
同様に本記事では、社会的な繋がり数を抑制することで、大規模感染を避ける効果を可視化した.社会的繋がり数とは,今回の数理モデルで導入した $n_\mathrm{n}$ であり,シミュレーションで言えば周囲の人の人数である.実際の社会に当てはめるならば家族との接触,職場や学校,「アフター・ファイブ」の諸活動など広い意味での他人との接触数である.この数値にも結果は鋭敏である.
(3)「活動の影響」の可視化
また本記事では,接触数を下げると同時に,「不要不急の移動」をしないことで,大規模感染を避ける効果を可視化した.移動の意味は物理的な移動も含むが,シミュレーションでは,社会的な結合の繋ぎ換えに対応する.このため参加するコミュニティや活動を次々と変化させること,と捉えることができるだろう.仮に一つ一つのコミュニティや活動規模が小さかったとしても,実質的な接触数の増加に繋がるからである.
いずれも理由は明らかであるし,よく言われている対策である.その効果の程が実感できない方が多かったのではないかと思う.今回のシミュレーションでそれらの効果が、少しでも分かりやすく可視化できたのであれば幸いである.個人の僅かな「行動変容」の積み重ねが,社会全体に大きな結果となって跳ね返ってくる.このことを一人ひとりが意識する上で、このシミュレーションがいささかでも役に立つことを願う.
本記事の執筆のヒントおよび機会を与えて下さいました京都女子大学の水野義之名誉教授に感謝いたします.
- 門 信一郎「この感染は拡大か収束か:再生産数 R の物理的意味と決定 ~単純なモデル方程式に基づく行動変容の判断のために~」https://rad-it21.com/サイエンス/kado-shinichiro_20200327/
# {newplot1.rb, figure_only: true}
require "./helper.rb"
require "numo/gnuplot"
d = data_read("model_1_evo.dat")
Numo.noteplot do
set title: "Model 1[感染率:高]"
set xlabel: "Time"
set ylabel: "S, I, R"
set yrange: 0..1.05
set xrange: 0..100
set key: "bottom"
plot d[:t], d[:s], {with: 'l', lw: 2, lc: :black , title: 'S'},
d[:t], d[:i], {with: 'l', lw: 2, lc: "'red'", title: 'I'},
d[:t], d[:r], {with: 'l', lw: 2, lc: "'dark-green'", title: 'R'}
end
# {ode.rb, figure_only: true}
require "~/lib/ruby/ode.rb"
alpha = 0.1
gamma = 0.1
neighbour = 4.7
# 初期値
irate = 0.01
initial_value = Numo::DFloat[1-irate, irate]
# 微分法知識
func = ->(x,t) {
s = x[0]
i = x[1]
dsdt = -alpha*neighbour * s * i
didt = alpha*neighbour * s * i - gamma * i
Numo::DFloat[dsdt, didt]
}
# 時間積分
tmin, tmax = 0.0, 256.0
tvec, xvec = ODE::RK4::solve(initial_value, tmin, tmax, 400, &func )
time = tvec.to_a
srate = xvec[true,0].to_a
irate = xvec[true,1].to_a
rrate = srate.zip(irate).map{|s,i| 1-s-i}
#
time_s = []
srate_s = []
irate_s = []
rrate_s = []
open("model_1_evo.dat").readlines.each do |ln|
tmp = ln.chomp.split(" ").map(&:to_f)
time_s << tmp[0]
srate_s << tmp[1]
irate_s << tmp[2]
rrate_s << tmp[3]
end
# グラフにする
require 'numo/gnuplot'
Numo.noteplot do
set title: "SIR model, Simulation (Model 1[感染率:高])"
set xlabel: "Time"
set ylabel: "S, I, R"
set yrange: 0..1.05
set xrange: 0..100
set key: "bottom"
plot time, srate, {with: 'l', lw: 2, lc: 'black', title: 'S(SIR model)'},
time, irate, {with: 'l', lw: 2, lc: '"red"', title: 'I(SIR model)'},
time, rrate, {with: 'l', lw: 2, lc: '"dark-green"', title: 'R(SIR model)'},
time_s, srate_s, {with: 'p', pt: 1, lc: '"black"', title: 'S(simulation)'},
time_s, irate_s, {with: 'p', pt: 1, lc: '"red"', title: 'I(simulation)'},
time_s, rrate_s, {with: 'p', pt: 1, lc: '"dark-green"', title: 'R(simulation)'}
end
# {ode2a.rb, figure_only: true}
require "~/lib/ruby/ode.rb"
require "./helper.rb"
def calc_model(alpha, gamma, neighbour)
# B=i4|CM
irate = 0.01
initial_value = Numo::DFloat[1-irate, irate]
# BHyJ,K!CN<1
func = ->(x,t) {
s = x[0]
i = x[1]
dsdt = -alpha*neighbour * s * i
didt = alpha * neighbour * s * i - gamma * i
Numo::DFloat[dsdt, didt]
}
# B;~4V@QJ,
tmin, tmax = 0.0, 256.0
tvec, xvec = ODE::RK4::solve(initial_value, tmin, tmax, 400, &func )
time = tvec.to_a
srate = xvec[true,0].to_a
irate = xvec[true,1].to_a
rrate = srate.zip(irate).map{|s,i| 1-s-i}
return time, srate, irate, rrate
end
def get_sim_data(fn)
d = data_read(fn)
time_s = d[:t]
srate_s = d[:s]
irate_s = d[:i]
rrate_s = d[:r]
return time_s, srate_s, irate_s, rrate_s
end
alpha = 0.05
gamma = 0.1
neighbour = 4.7
fn = "model_2_evo_1.dat"
time_s, srate_s, irate_s, rrate_s = get_sim_data(fn)
time, srate, irate, rrate = calc_model(alpha, gamma, neighbour)
require 'numo/gnuplot'
Numo.noteplot do
set title: "SIR model, Simulation (Model 2[感染率:中])"
set xlabel: "Time"
set ylabel: "S, I, R"
set yrange: 0..1.05
set xrange: 0..100
set key: "right center"
plot time, srate, {with: 'l', lw: 2, lc: 'black', title: 'S(SIR model)'},
time, irate, {with: 'l', lw: 2, lc: '"red"', title: 'I(SIR model)'},
time, rrate, {with: 'l', lw: 2, lc: '"dark-green"', title: 'R(SIR model)'},
time_s, srate_s, {with: 'p', pt: 1, lc: '"black"', title: 'S(simulation)'},
time_s, irate_s, {with: 'p', pt: 1, lc: '"red"', title: 'I(simulation)'},
time_s, rrate_s, {with: 'p', pt: 1, lc: '"dark-green"', title: 'R(simulation)'}
end
# {newplot3.rb, figure_only: true}
require "./helper.rb"
require 'numo/gnuplot'
dat = data_read("model_3_evo.dat")
# GNUPLOTで表示する
# 時間
Numo.noteplot do
set title: "Model 3[感染率:低]"
set xlabel: "Time"
set ylabel: "S, I, R"
set yrange: 0..1.05
set xrange: 0..100
plot dat[:t], dat[:s], {with: 'l', lw: 2, lc: "'black'", title: 'S'},
dat[:t], dat[:i], {with: 'l', lw: 2, lc: "'red'", title: 'I'},
dat[:t], dat[:r], {with: 'l', lw: 2, lc: "'dark-green'", title: 'R'}
end
# {newplot1-3.rb, figure_only: true}
require "./helper.rb"
require 'numo/gnuplot'
d1 = data_read("model_1_evo.dat")
d2 = data_read("model_2_evo.dat")
d3 = data_read("model_3_evo.dat")
# GNUPLOTで表示する
# 時間
Numo.noteplot do
set xlabel: "Time"
set ylabel: "S"
set yrange: 0..1.05
set xrange: 0..100
set key: "right center"
plot d1[:t], d1[:s], {with: 'l', lw: 2, title: 'Model 1[感染率:高]'},
d2[:t], d2[:s], {with: 'l', lw: 2, title: 'Model 2[感染率:中]'},
d3[:t], d3[:s], {with: 'l', lw: 2, title: 'Model 3[感染率:低]'}
end
# {newplot1-4.rb, figure_only: true}
require "./helper.rb"
require 'numo/gnuplot'
d1 = data_read("model_1_evo.dat")
d4 = data_read("model_4_evo.dat")
# GNUPLOTで表示する
# 時間
Numo.noteplot do
set xlabel: "Time"
set ylabel: "S"
set yrange: 0..1.05
set xrange: 0..100
set key: "bottom"
plot d1[:t], d1[:s], {with: 'l', lw: 2, title: 'Model 1[感染率:高]'},
d4[:t], d4[:s], {with: 'l', lw: 2, title: 'Model 4[接触数:低]'}
end
# {newplot4-5.rb, figure_only: true}
require "./helper.rb"
require 'numo/gnuplot'
d4 = data_read("model_4_evo.dat")
d5 = data_read("model_5_evo.dat")
# GNUPLOTで表示する
# 時間
Numo.noteplot do
set xlabel: "Time"
set ylabel: "S"
set yrange: 0..1.05
set xrange: 0..100
set key: "bottom"
plot d4[:t], d4[:s], {with: 'l', lw: 2, title: 'Model 4[接触数:低]'},
d5[:t], d5[:s], {with: 'l', lw: 2, title: 'Model 5[移動:あり]'}
end














[…] すが、感染対策が出来ていると感染率が低いため、やがて終息する。(100×100の格子シミュレーションの結果)” https://rad-it21.com/%E3%82%B5%E3%82%A4%E3%82%A8%E3%83%B3%E3%82%B9/michikoshi-shugo_20200331/ […]