100個の数字が意味するもの
前回は将棋ソフトボナンザの分析や簡単な例題を通して、いま盛んに喧伝されている「AI」が、実は機械学習というAIの研究分野の中ではごく一分野のものにすぎず、AI研究から見るとむしろ脇道であり、「知能」の実現という状態からは程遠いということを述べた(決して機械学習の研究を見下しているわけではなく、立派な学問分野だと思いますが、機械学習をAIの代表のようにいうのは間違っていると言いたいだけです)。
今回は、ごく簡単な例を用いて、機械学習が実際にどんなことをしているか体験しよう。ここに図のような1〜10までの数字が10×10のマス目に100個並んでいる表があるとする。
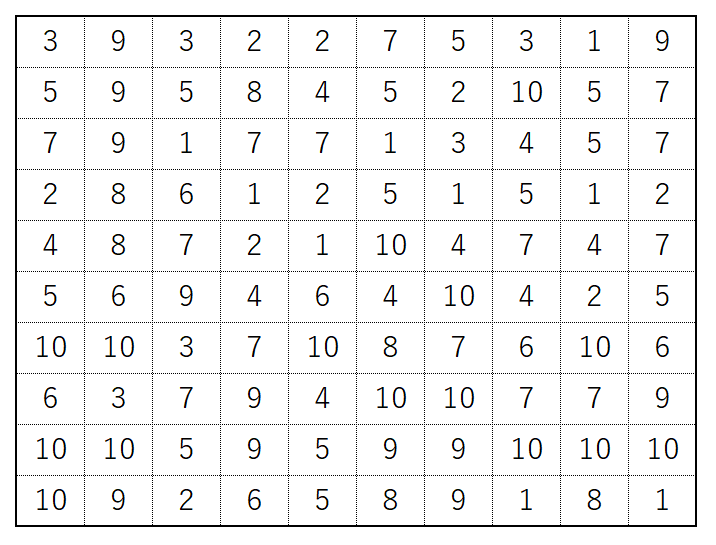
実はこの表はあるルールに基づいてとある自然数を表現することになっているとする。その数はこの表の場合は2393であるが、別の10×10の100個の数字が与えられれば、その表が表現する自然数も異なる。100個の数字が提示された場合、ルールで決まる自然数を当てよ、という問題を解くことは可能であろうか。
実はそのルールは簡単である。10×10のマス目のうち、左上の4つの数(3932)を逆の順番に並べただけだ。
数学的な表現をすれば「10×10個の数字のうち、一列目の左から4つの数字をN1,N2,N3,N4とする。このとき、この100個の数字が表現する自然数は、1000×N4+100×N3+10×N2+N1とする」というだけである。
答えを言われてしまえば簡単だが、その答えを見つけるのは簡単ではない。2,3,9という三種の数字は左上の4つの数字以外にもたくさん出てくる。そもそも、10,100,1000をかける、などという単純なルールで作られているなんてそうそう簡単に思いつかないだろう。
連立一次方程式と機械学習
だが、この問題は実は「100個のうちの何個かの数字を選び、それぞれにある数をかけて足し合わせることで作られている(条件[*])」という情報が与えられれば(何個の数字を選ぶのか、とか、どんな数を掛けるのか、という情報が全く無くても)簡単に解けることが知られている。
それは「連立一次方程式」という方法で高校の数学で誰もが普通に学ぶ、それほど高度でもない数学である。具体的には100個の数字と、その数字が表す自然数の組が100組あれば答えを出せることが知られている(厳密なことをいうと100組で「必ず」うまく行くとは言えないのだがその話をする余裕はないので割愛する。しかし、殆どはうまくいく)。
さて、それでは連立一次方程式を知らず、条件[*]の情報だけは知っていて、目の前に電卓があり、時間制限がない場合、どうすればいいだろう?
多分、多くの人は「でたらめに数字を選んで適当な数をかけてみて、試行錯誤を繰り返し正解に達するまで頑張る」という方法を取るだろう。従来型の、人間のサポートをもらっている機械学習がやっていることはまさにこれである。
人間よりコンピュータは圧倒的に速いのでこんなうろんな方法でもかなりいい答えを出すことができる。その代わり、ずっと大量のデータを必要とする。
連立一次方程式を使えば、100個の数と答えの自然数の組は100組あればよかったが、この「試行錯誤」で連立一次方程式と遜色ない精度をだそうとすると、なんと100倍の一万組の100個の数と自然数の答えの組が必要になる(厳密なことをいうと100組でもできないことはない。ただし、その場合、とんでもない長い時間がかかる)。
この例が教えていることは、機械学習は「正しい答えの出し方(この場合は連立一次方程式)」を知らなくても、人間がある程度のヒント(この場合は条件[*])を渡せば、十分実用性のある答えに到達できる、ということ、ただし、そのためには「正しい答えの出し方」を知っている場合に比べて、ずっとたくさんのデータ(この場合は100個の数と答えの自然数の組)を必要とする、ということである。
新世代型の機械学習
しかし、これはまだボナンザに相当する、旧世代の機械学習のレベルである。
ボナンザが人間に「どの局面とどの局面を似ているとみなすか」の基準を教えてもらわないといけなかったのと同じように、この機械学習は条件[*]の情報を必要とした。この機械学習には限界があるのは明らかだ。
条件[*]の情報が正しくなければ、例えば、本当のルールは条件[*]ではなく「100個のうちの何個かの数字を選び、『二乗してから』それぞれにある数をかけて足し合わせる」というルールだとしたら(つまり、人間の指示が間違っていれば)、条件[*]を前提とするこの機械学習は正しい答えを出すことはできないだろう。
新世代型の機械学習は条件[*]の情報をもらわなくても、100個の数字と、自然数の組をもらっただけで、良い精度で答えをだすことができる。ただ、その場合、必要な組の数は更に増え(10万組)、試行錯誤の回数も10万回という膨大な回数になる(上では言及しなかったが、条件[*]を与えた機械学習では一万組のデータで200回程度の試行錯誤すれば十分な精度に到達する)。
さらに、本当の答えを知らないのだから仕方ないとはいえ、誤差は決してゼロにならず、3%程度の誤差が必ず残ってしまう。97%の精度で自然数を予測できるなら十分な精度とも言えるが、この誤差をゼロにする方法はない。条件[*]の様な情報がなくても答えを出せるという利点の裏側で、決して誤差がゼロにならない、という問題点が発生する。
この例は実に単純な例ではあるが、どんな文字でも画像でも音でも、コンピュータの中ではただの数字に変換されて処理されているということを考えれば、これと同じ方法で、画像認識や機械翻訳や囲碁・将棋・チェスのプログラムも作れることは想像に難くないだろう。
機械学習はそのすべてを同じように数字対数字の問題として扱っているだけである。条件[*]を知らずに機械学習がどうやって97%の精度を達成したのかは、人間にも機械学習のプログラムにもわかりようがない(正確にはなんらかの数式は作られているのだからそれをトレースすることは可能である。ただ、その数式は複雑すぎて人間に理解できるようなものではもはや無くなっている)。
この単純な例から、我々はいろいろなことを学べるだろう。
機械学習は何かを考えているわけではなく、数字と数字の間の対応関係をなるべくよく表現する複雑な数式を作る能力を持っていること、その数式を導くためには、「正しい答えの出し方(この場合は連立一次方程式)」を知っている場合に比べてずっと膨大な(今の例では100の1000倍が10万なので1000倍のデータ)が必要なこと、そして、(本当の答えを知らないので)けっして誤差はゼロにはならないこと、などである。

知能には程遠いという現実
こんなうろんなことをしている機械学習が人間の知能を模倣できようもないのは明らかだろう。いま、盛んに喧伝されているいわゆるシンギュラリティなるものは今の技術の延長上にあるものではなく、将来的にいまのペースでAIの研究が発展し、革命的なことが起きたら、という前提での話なのだ。
一方で膨大なデータとそれを扱う高速な計算機さえあれば、本当の意味での人工知能なしには難しいと思われたこと、自動運転や機械翻訳や、囲碁の世界チャンピオンに勝つ、といったことが可能になったのもまた事実である。
この新世代型の機械学習の代表は深層学習(あるいはディープラーニング)と呼ばれているものである。
残念ながら人類はまだなぜ深層学習がこんなに高性能なのかをまったく理解できていない。そのおかげで3%の誤差がどんなときに起きるかもわからない。
だが、なんだか機械学習が突然進歩したようにみえるのは、つい最近まで、計算に使える膨大なデータは無かったし、また、それを扱う大きなメモリーを備えた高速の計算機も無かったからだ。
実際、深層学習の基本的な理念であるニューラルネットワークという技術は40年前からあった。その古い技術を時代の寵児に押し上げたのは、可能性を信じて諦めなかった少数の科学者の信念と、飛躍的に進化したインターネットと計算機のおかげなのである。
まとめると、今の機械学習は膨大なデータが収集できない分野には無力である。また、同時に何かを考えているわけはないので、完全に人間の知能を代替することはできない。
そして、そのために、100%の精度は決して実現できない、ということだ。
次回は、この内容を踏まえて、AI=機械学習の今後の問題点と可能性について論じよう。
<「AI=機械学習とは何か(Ⅰ)」へ
>「AI=機械学習とは何か(Ⅲ)」へ
※本稿は筆者が中央大学学員会(OB会)学術講演会で行った講演、「AI(人工知能)の過去・現在・未来―AIは人間を超えるのか―」に基づいている。同講演で使用したプレゼンテーションと講演ビデオは
http://www.granular.com/gakujutsu/
で公開されている。
この原稿の記述は機械学習についての知識がほぼゼロである聴衆を想定したものであり、ある程度、知識がある読者には物足りなく、あるいは、不正確な記述が目につくかもしれない。以下、いくつかの補足情報を付記する。
深層学習については、例えばWikipediaの
https://ja.wikipedia.org/wiki/ディープラーニング
を眺めた上で、
深層学習 site:ac.jp
等で検索すると、大学生レベルの資料が多く見つかる。















