はじめに
「量子ウォーク(quantum walk)」は「ランダムウォーク(random walk)」の量子版として,2000年頃より本格的に研究され始めた新しい数理モデルです.
ランダムウォークは,拡散現象,ノイズを含む問題など,様々な分野での現象を記述し解析するために必要であり,非常に重要な役割を担っています.一方,量子ウォークは,量子系においてそのような立場になりえる可能性が強く期待されており,大変活発に研究されています.
ご存知のように,革新技術の一つとして,まだ一般的な実用化には至っていませんが量子力学の法則に従って動く「量子コンピュータ」があります.量子ウォークは,この量子コンピュータの研究周辺からも研究が行われているのです.2019年10月にネイチャー誌から発表されたグーグルの量子超越実験の結果(量子超越性,quantum computational supremacy)が,またたく間に世界を駆け抜ける程のニュースになったことはまだ記憶に新しいところです.つまり,量子コンピュータを用いれば,古典コンピュータでは出来ないことを実現できるかもしれない時代が近づいてきたことを予感させるような,ある意味衝撃的な実験結果でした.
さて,このような状況を踏まえ本稿では,まず量子ウォークの古典版であるランダムウォーク周辺の話題を少し詳しくお話しします.次に,その量子版として量子ウォークはどこが違うのかに触れつつ,ランダムウォークから量子ウォークに至る一つの道程を解説したく思います.
ランダムウォークとは
まず,物理学,化学,生物学,工学,経済学など様々な分野で大変重要な役割をしている「ランダムウォーク」について簡単に説明をしていきましょう.
このランダムウォークは,粒子が「でたらめに動きまわる」数学のモデルなので,その訳は,酔っ払い(ランダムウォーカー)の千鳥足の動きに似ていることにより「酔歩(すいほ)」,或いは,「乱歩(らんぽ)」と呼ばれることがあります.
はじめに,酔っ払いが動く空間をd次元の格子で考えます.このd次元の格子とは,1 次元では直線上の格子(図 1 参照),2 次元では平面上の格子のことです(図 2 参照).そして,酔っ払いがその空間の上を「ふらふらと」動くのです.その動きまわるルールをもう少し正確に説明しましょう.
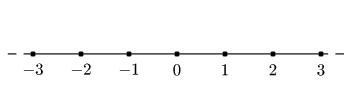 図1:1次元格子
図1:1次元格子
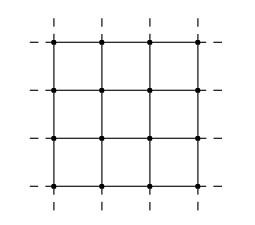 図2:2次元格子
図2:2次元格子
1 次元の場合には,ワンステップごとに左と右に等しい確率,1/2 で動きます.例えば,ランダムウォーカーが原点の場所から出発するとして,まず偏りの無いコインを投げます.表が出たら左に,裏が出たら右に1単位だけ動くとします.そして,ステップごとに,同じコインを投げて動く方向を決めていきます.次に 2 次元の場合は,前後左右に等しい確率 1/4 で移動します.3 次元の場合は,前後左右の他に上下が加わり,それぞれに等しい確率 1/6 で動きます.この場合は,ステップごとにサイコロをなげる場合に対応します.もっと一般にd次元の場合も同様に考えられ,その場合には最も近いところにある 2d個の格子点に等しい確率,つまり,1/2dで移動します.ここで一言注意です.ランダムウォークも量子ウォークも本稿ではワンステップごとに時間発展する「離散時間」のモデルを扱います.実は「連続時間」のモデルもありますが,多くの場合に(特にランダムウォークでは)定性的な結果は変わらないので割愛します.
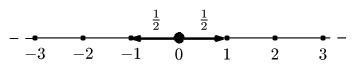 図3:1次元ランダムウォーク
図3:1次元ランダムウォーク
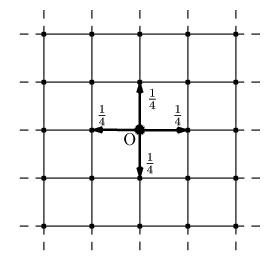 図4:2次元ランダムウォーク
図4:2次元ランダムウォーク
このように,最も近い格子点に等しい確率で動くランダムウォークは「単純」ランダムウォークとも呼ばれます(以下,「単純」を省略しましょう).また,動きを定める確率に偏りが無いので,このようなモデルは「対称な」ランダムウォークと呼ばれます.一方,そうで無い場合は「非対称な」ランダムウォークです.
例えば,1 次元の場合,もっと一般に,左に確率 p,右に確率 q で動く場合が考えられます.但し,p と q を加えると 1 とします.最初の対称な例は,p も q も 1/2 の場合でした.また,p が 1/2 でないと(従って,足して 1 なので,q も 1/2 にはなりませんが)対称ではないので非対称なランダムウォークになります.以下特に断らなければ,「対称な」場合を考えていると思って下さい.
さて,1,2 次元の場合には必ず出発点に戻ってきます(もう少し正確に言いますと,有限な時間に再び戻ってくる確率が 1 ということです).このような場合,そのランダムウォークは「再帰的」と言い,そうでないときは,「非再帰的」と呼ばれます.また,再帰的なときは,戻ってきてはリセットすることにより,実は必ず無限回戻ってくることも分かります.ところが 3 次元以上になると,非再帰的になり必ずしも戻ってくるとは限らないのです.酔っ払いは家に戻ってこられるが,酔っ払いの鳥は巣に戻ってこられない,とも言えるかもしれません.では,雑居ビルをふらついている酔っ払いはどうでしょうか?
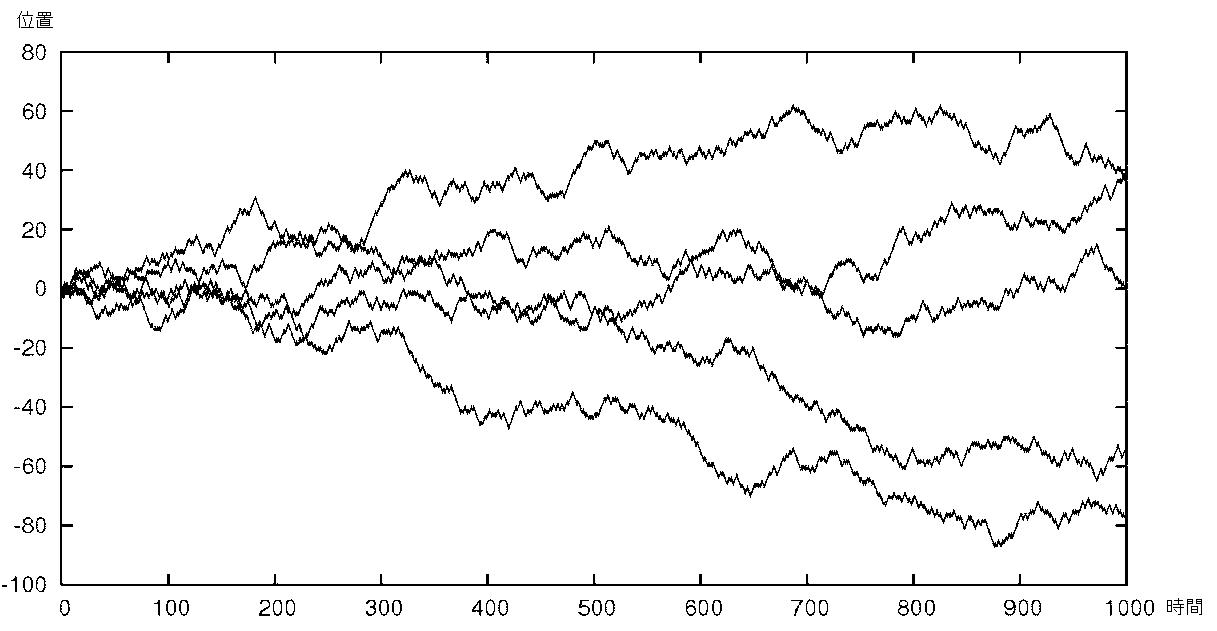 図5:1次元ランダムウォーク(原点から出発した 5 人のランダムウォーカーの軌跡)
図5:1次元ランダムウォーク(原点から出発した 5 人のランダムウォーカーの軌跡)
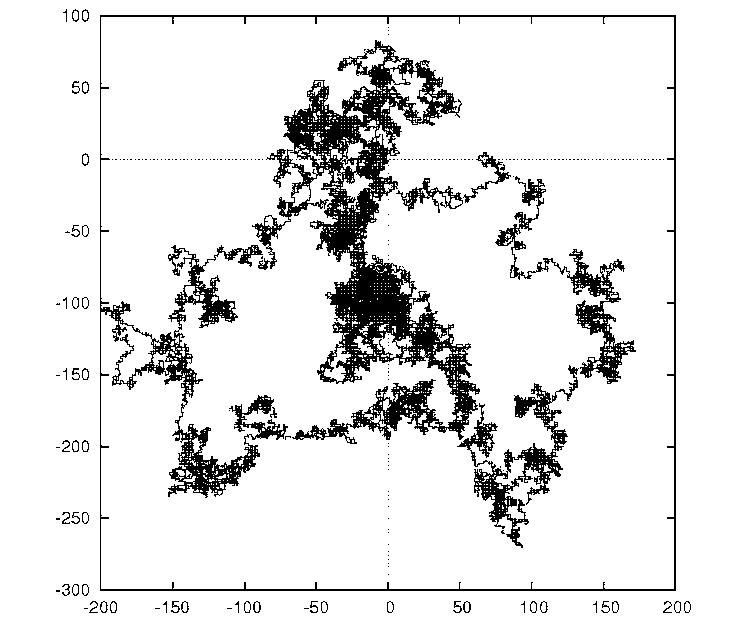 図6:2次元ランダムウォーク(原点から出発した 1 人のランダムウォーカーの軌跡)
図6:2次元ランダムウォーク(原点から出発した 1 人のランダムウォーカーの軌跡)
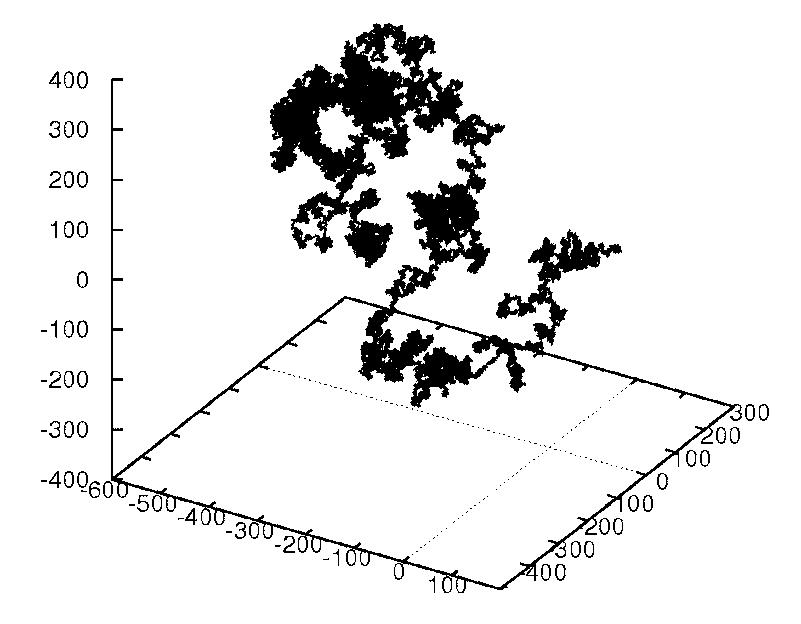 図7:3次元ランダムウォーク(原点から出発した 1 人のランダムウォーカーの軌跡)
図7:3次元ランダムウォーク(原点から出発した 1 人のランダムウォーカーの軌跡)
上記の 1 次元,2 次元は再帰的で,3 次元以上では非再帰的という結果は1921年に数学者ポーヤ(G.Polya)によって示されました.彼がチューリッヒ近郊の公園を散策しているとき,同じ若いカップルにたびたび会うのでこのような問題を考えたと言われています(逆に若いカップルが,ポーヤに気がついたかどうかは知られていません).実は,どんな次元でも(勿論 1 次元でも)非対称な場合には,非再帰的になることも示せます.例えば酔って転んで歩き方に偏りが出てくると,一定の方向に動き易く,出発した場所に戻りづらくなるのです.
グラフ上のランダムウォーク
d次元格子上のランダムウォークの再帰性について最初に述べましたが,それ以外の様々なグラフ上のランダムウォークについても同様に定義することができます.そして,そのランダムウォークが再帰的か,或いは,非再帰的かを場合によっては示すことができます.逆にそのことを示すことが,グラフの性質を決めることになるのです.例えば,図 8 の三角格子の場合には再帰的,図 9 のケーリー・ツリーの場合には非再帰的になります.
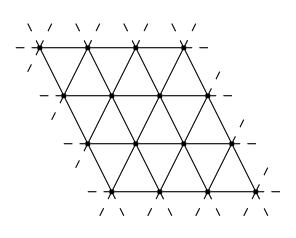 図8 :三角格子
図8 :三角格子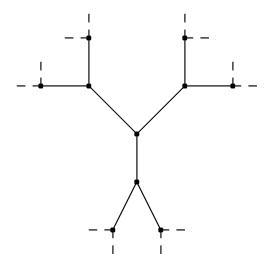 図9 : ケーリー・ツリー
図9 : ケーリー・ツリー
投票者モデルとランダムウォーク
さてランダムウォークの再帰性と非再帰性は,意外なことに選挙の数理モデルと密接に関係しています.この「投票者モデル(voter model)」は,1973年にクリフォード(P.Clifford)とサドバリー(A.Sudbury),1975年にホリー(R.Holley)とリゲット(T.M.Liggett)によってそれぞれ独立に導入されました.例えば,アメリカの共和党と民主党のように,A,Bの2つの政党だけを扱う場合を考えましょう.そして各支持者は考えているグラフの格子点上に存在するとします.図 10 のように,A党支持者は,周りの人がB党支持者であればあるほど,B党に鞍替えし易く,逆にB党支持者は,周りの人がA党支持者であればあるほど,A党に鞍替えし易いとします.少し説明すると,図 10 の場合は,左辺はA党支持者の周りにB党支持者が 3 人いて,右辺は 2 人いるので,左辺の方が右辺に比べてA党からB党に鞍替えする確率が高くなります.つまり,周りの様子を意識して,日和見的に意見をころころ変えるような状況です.
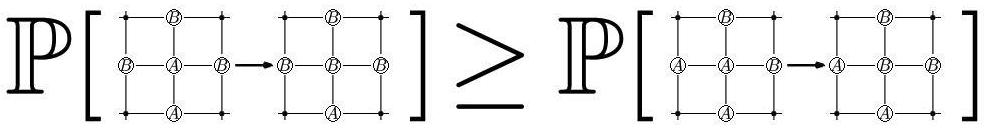 図10: 2 次元格子上の投票者モデルのルール(Pは確率を表します)
図10: 2 次元格子上の投票者モデルのルール(Pは確率を表します)
そして初期条件として,A党支持者とB党支持者が半分ずつばらばらに存在していたとすると,充分時間が経た後に,格子の次元が2以下の場合には,A党支持者だけの世界かB党支持者だけの世界になってしまいます.一方,格子の次元が3以上の場合には,A党支持者とB党支持者が共存する世界になります.
この違いは,空間の次元が低いと,例えば,1次元の場合には隣の人は2人,2次元の場合には隣の人は4人なので(一般には d次元では隣の人数は2d人です),隣人の数が少なく,ある意味でつながり方が濃くなり,意見が一方に偏りやすくなってしまうからです.それに対して,空間次元が高いと,色々な人がまわりにいる傾向が強いので,多様なつながり方があって,意見が一つに集約されにくく,共存状態が起こりやすくなるのです.ラフに言えば,様々なコミュニケーションが可能なつながりを持ち得る状況では,意見の多様性が保たれることになります.
実はこのような異なる意見の共存・非共存を決めるのは,モデルの定義されている空間,この場合には,d次元の格子ですが,その上を動きまわるランダムウォークの再帰性と非再帰性であることが証明されています.具体的には,投票者モデルの場合には,その共存と非共存が,そのモデルが定義されている同じ空間上でのランダムウォークの再帰性と非再帰性に,表のように完全に対応しているのです.
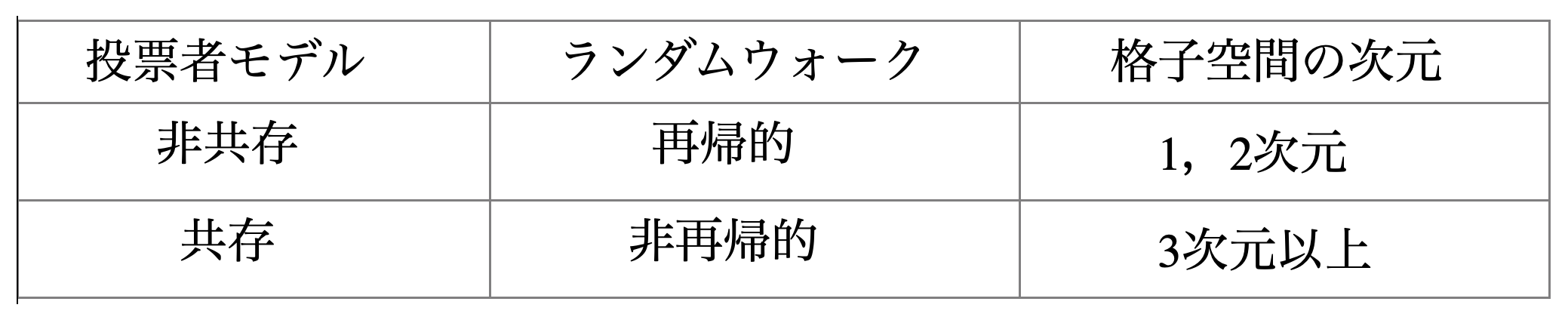
直感的に上に述べたことを説明しますと,投票者モデルの時計の針を未来から過去に逆に動かし,現在の意見を持つに至った経緯を追跡します.このような様子は「双対プロセス」と一般には呼ばれますが,この場合には「合体的ランダムウォーク」がその双対プロセスになります.具体的には沢山の酔っ払いが動き回っているのですが,2 人の酔っ払いがぶつかると合体して 1 人になるのです.
空間の次元が小さいと再帰的なので酔っ払いがぶつかり易く,最初に有限の人数の酔っ払いから出発すると,最終的には1 人の酔っ払いになってしまいます.このことが,充分時間が経つと,共和党か民主党のどちらか一方の政党になってしまうことに対応します.その背景の性質として,1次元ランダムウォークの広がりを表す標準偏差は時刻の平方根に比例しますが,d次元の場合にはそのd乗になり,広がりやすく遠くに移動する傾向が強くなります.一方,空間の次元が大きいと今度は再帰的では無いので酔っ払いはぶつかりづらく,いつまでも多数の酔っ払いが動き回っている状態が生じます.これが共和党か民主党のどちらか一方にならない共存状態に対応するのです.
実際の社会では,格子のようには空間の構造が良く分からない場合が多いのですが,都市部では空間の次元が大きく,農村部では空間の次元が小さい傾向にあると言えるかも知れません.
量子ウォークとは
さて,これから多少専門的になりますが,量子ウォークについて説明しましょう.
ランダムウォークは,本稿の最初でも触れた通り,様々な分野での古典的な現象を記述し解析するために非常に重要な役割を担っています.また,量子ウォークは量子モデルに対してそのような立場になりえる可能性が強く期待されているモデルです.
量子ウォークは,量子モデルとしては比較的簡単に定義できるモデルなので,ファインマン(R.P.Feynman)をはじめとし,おそらく多くの人達によって同様のモデルが提案されてきたと思われます.量子ウォークへのアイデアを提案した文献として頻繁に引用されるのは,1993年の アハロノフ(Y.Aharonov)達の論文です.アハロノフは,アハロノフ-ボーム効果や弱測定の研究で大変有名な物理学者です.そして,量子情報科学周辺分野の2001年のアンバイニス(A.Ambainis)達の論文などが契機となって,量子ウォークの研究が開花したといっても過言ではありません.
実は,それらの前後に,例えば,1988年のガダー(S.P.Gudder)による著書『Quantum Probability』では量子ウォークのモデルが定義され,簡単な性質が紹介されています.同様に,1996年頃に量子ゲームの発案者としても知られているメイヤー(D.A.Meyer)も同じモデルを量子セルオートマトンとして提案し,2 年ほど関連の論文を出ましたが進展はありませんでした.このように現れては消えていった量子ウォークは,最終的には量子コンピュータの研究が追い風となり,上記 2001年のアンバイニス達の本格的な研究論文などで,多数の目にとまるようになったのです.
量子ウォークの定義は粗く言うと,ランダムウォークの移動を定める「確率」の代わりに,量子ウォークの場合は「行列」を考えるのです.この行列は「量子コイン」と呼ばれることもあります.確率は「実数」ですから「可換」ですが,「行列」は一般に「非可換」です.つまり,実数 a,b に対して,ab=ba が成立しますが,行列 A,B に対して,AB=BA は必ずしも成り立ちません.この非可換の関係から,量子の性質の一つが立ち現れます.量子ウォークの定義の詳細は準備が必要なので,本稿最後の参考文献で紹介されている本を参照して頂きたく思います.
筆者の量子ウォークと出会いは,2002年の正月に,検索サイトに偶然打ち込んだ「quantum random walk」(当時はそう呼ばれていました.)により,ネット上に数編しかなかった論文がヒットしたことによります.単純そうですが,一見するとわかりづらい定義の“量子ウォーク”なるものに興味を持ちました.なぜなら,ランダムウォークの量子版といわれて導入されたこのモデルが,ランダムウォークと異なる性質をもっていたからです.
1 番目は,ランダムウォークの確率分布(確率測度)が 2 項分布で表され,出発点の確率が高い単峰型であるのに対し,量子ウォークの確率分布は,粗くいうとその逆の,出発点の確率が最も低く,2 つの端点に近い場所の確率が高い逆釣鐘型であることです.
図11 で 1 次元の量子ウォークとランダムウォークの確率分布の違いを示しました.ここでは,1次元量子ウォークの典型的なモデルとして,アダマールウォークを採用します.図を見るとわかるように,点線で示したランダムウォークの場合は,出発点の原点に存在する確率が最も高いのですが,実線で示した量子ウォークの場合には逆に,出発点の原点に存在する確率は低く,両端付近に高いピークがあります.そのために,量子ウォークでは 1次元でも出発点に戻りづらく,遠方に存在する確率が高くなります.言い換えると,1 次元でも量子ウォークの場合には「非再帰的」になりえるのです.
この量子ウォーカーは,左へのジャンプと右へのジャンプの 2 状態を持つので,1 次元 2 状態量子ウォークと考えられます.つまり,内部自由度が「左」と「右」の「2」つあるとも言えます.一方,ランダムウォークの内部自由度は「1」で,この内部自由度が 2 以上あることは,定常測度(時刻に対して不変な測度)を求めるアプローチなど,色々な場面での差異の原因となり得ます.
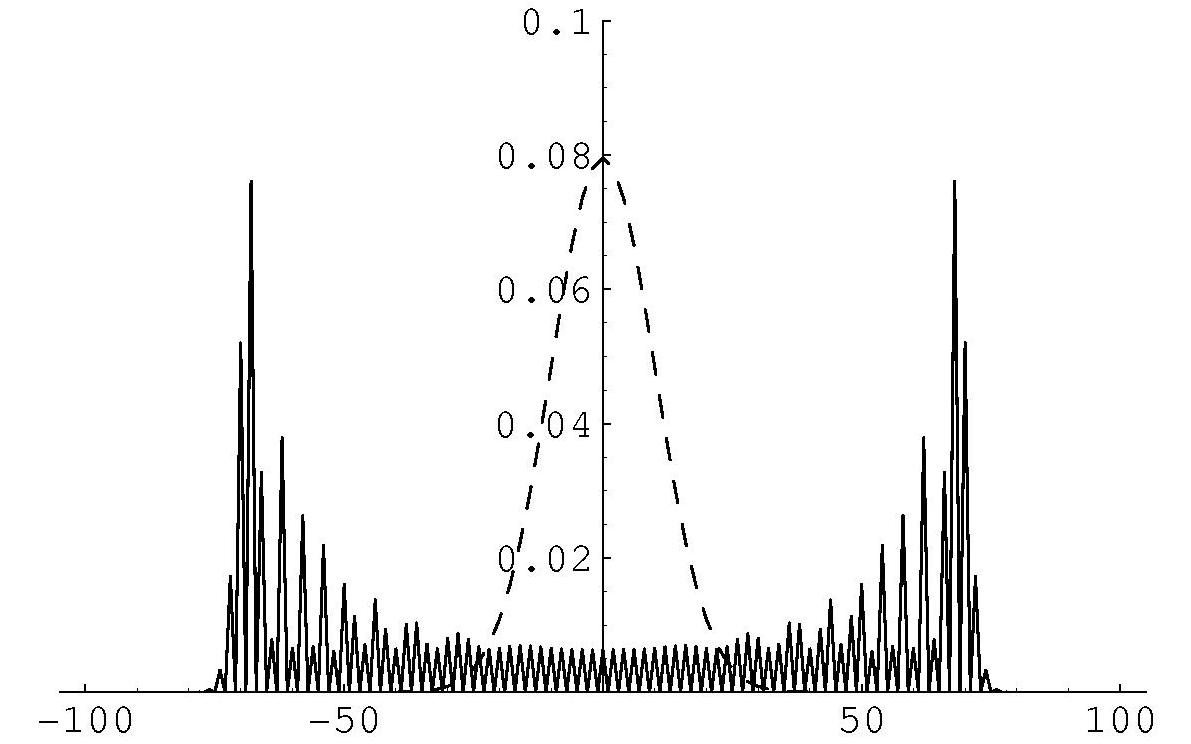 図11:1次元の量子ウォーク(実線)とランダムウォーク(点線)との確率分布の違い
図11:1次元の量子ウォーク(実線)とランダムウォーク(点線)との確率分布の違い
そして,2 番目は,ランダムウォークの標準偏差が時刻の平方根に比例するのに対して,量子ウォークの場合は時刻に比例することです.このようなランダムウォークよりも遠くに移動できる広がり方は,時刻に比例するため「線形的拡散」とも呼ばれています.
量子ウォークは,上記のようなランダムウォークとの違いなどをうまく利用し,空間構造をもった探索問題,つまり,見つけたいターゲットの場所を高い確率で探す問題,への応用が試みられています.
2002年当時,まだ本格的な研究がはじまった時期だけに,確率分布の明示的な表現やランダムウォークの中心極限定理(確率論の基本定理の一つ)に対応する弱収束極限は知られていませんでした.いまや 1 次元系の基本的な結果となりましたが,組合せ論的な手法で弱収束極限を得ることに著者は成功し,2002年の6月には第一報を投稿することができ,その後まとまった論文として完成させました.
今ではこの結果は,フーリエ解析,停留位相法,母関数法などさまざまな手法で求められています.一般に,量子ウォークの解析手法は,その他,転送行列法,グラフゼータ法,スペクトル写像定理,スペクトル散乱理論を用いた方法などがあります.
量子ウォークの性質
前節で,量子ウォークにはランダムウォークよりも遠方に移動する「線形的拡散」の性質を持つことを説明しました.実は,それとは相反するような,ランダムウォークに比べて出発点に留まり続けるという「局在化」の性質も持ちますので,それについて説明します.
このような,「線形的拡散」と「局在化」という相反する性質を同時に持つ典型的な量子ウォークとして,1 次元の3 状態モデルと2 次元の4 状態モデルがありますので,本節では,最初に前者のモデルを.次に後者のモデルを紹介しましょう.
さて「局在化」について説明するため,まず 1 次元 3 状態グローヴァーウォーク (Grover walk) を例に解説します.グローヴァーウォークは,1996年にグローヴァー(L.K.Grover)によって提案された量子探索アルゴリズムに関連するグローヴァー行列を量子コインとして用いるので,そのように呼ばれています.この量子ウォーカーは,左へのジャンプ,右へのジャンプだけだった 2 状態に加えて,同じ場所に留まる,合計 3 つの状態を持ちます.つまり,内部自由度が 3 になります.
初期状態として,量子ウォーカーが原点から出発する場合を考えます.そして,内部自由度が 3 なので,原点での量子状態は 3 成分を持つベクトルで表されます.量子ウォークの時刻を無限大にしてその極限測度が求まるとき,“局在化が起こる” とは,出発点での極限測度の値が 0 にならない場合をいいます(極限測度が存在しないときは,時間平均極限測度などを考えます).1 次元 3 状態グローヴァーウォークでは,局在化は起こり,さらに,原点からの距離に対して指数関数的に減少していることもわかります.一方,対応する1 次元 3 状態のランダムウォークでは,極限測度は全ての場所で 0 になり,つまり,局在化は起きません.
実際,図 12 を見るとわかるように,青線の 3 状態量子ウォークでは,図 11 の 2 状態量子ウォークのような確率分布の形をしていますが,出発点の原点近くの確率も高くなっているところが異なります.一方,赤線の 3 状態ランダムウォークは,図 11 の 2 状態ランダムウォークと同様の釣鐘型の確率分布の形をしています.そして時間が十分たつと,3 状態量子ウォークでは出発点も含め,全ての場所で確率が正の値として残り,3 状態ランダムウォークでは,全ての場所で確率が 0 になってしまうのです.
このように,局在化が起きることは,まさに量子ウォーク特有の性質になりますが,同時にこのモデルでは,相反するような線形的拡散も起こっているのが大変興味深い点です.
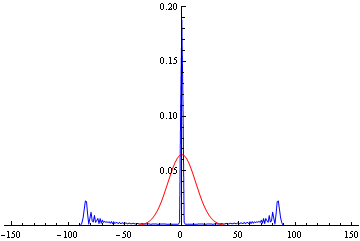 図12 :1 次元 3 状態の量子ウォーク(青線)とランダムウォーク(赤線)との確率分布の違い
図12 :1 次元 3 状態の量子ウォーク(青線)とランダムウォーク(赤線)との確率分布の違い
次に,2 次元で 4 方向に移動する 4 状態の量子ウォークについて紹介します.2 次元になると,図 13 (a,b,c) の確率分布のように,1次元と同様にランダムウォークより遠方に存在する確率が高い「線形的拡散」を持つモデルや,加えて,ランダムウォーク以上に出発点に留まり続ける確率が高い「局在化」という性質を示すモデルなど,様々な挙動をとる量子ウォークがあります.
ここでは,(a) から (c) まで,3つの異なる量子ウォーク((a) アダマールウォーク,(b) フーリエウォーク,(c) グローヴァーウォーク)の確率分布をそれぞれ示しました.ここでフーリエウォークとは,量子コインが離散フーリエ変換に関連する行列で定義されるモデルです.また,比較の為に,2 次元のランダムウォークの確率分布を図 14 に載せました.
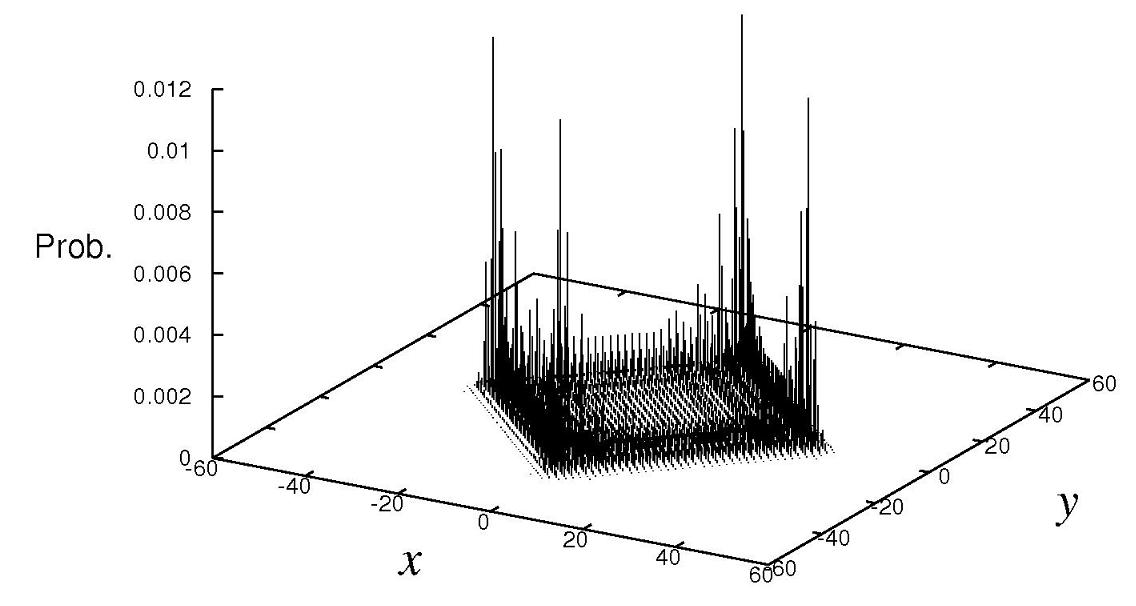 図13 (a) : 2次元アダマールウォーク(量子ウォーク)の確率分布
図13 (a) : 2次元アダマールウォーク(量子ウォーク)の確率分布
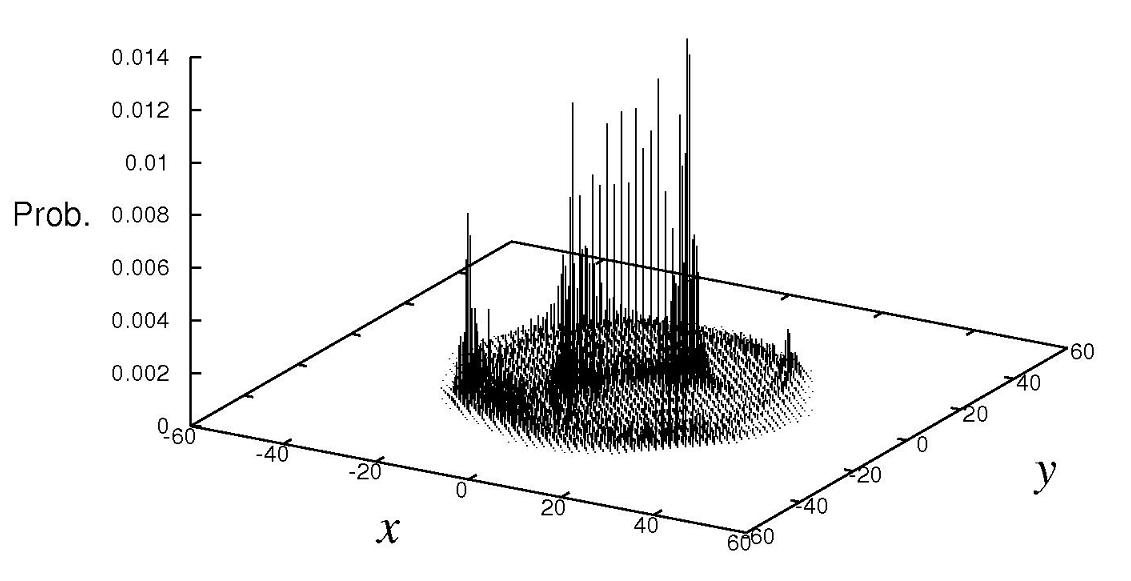 図13 (b) : 2次元フーリエウォーク(量子ウォーク)の確率分布
図13 (b) : 2次元フーリエウォーク(量子ウォーク)の確率分布
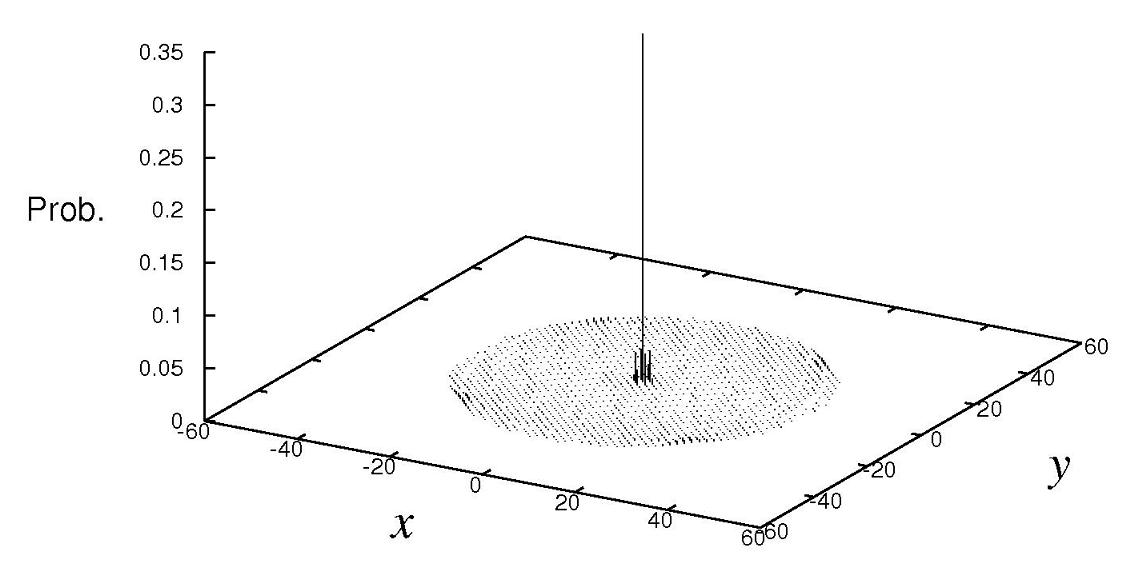 図13 (c) : 2次元グローヴァーウォーク(量子ウォーク)の確率分布
図13 (c) : 2次元グローヴァーウォーク(量子ウォーク)の確率分布
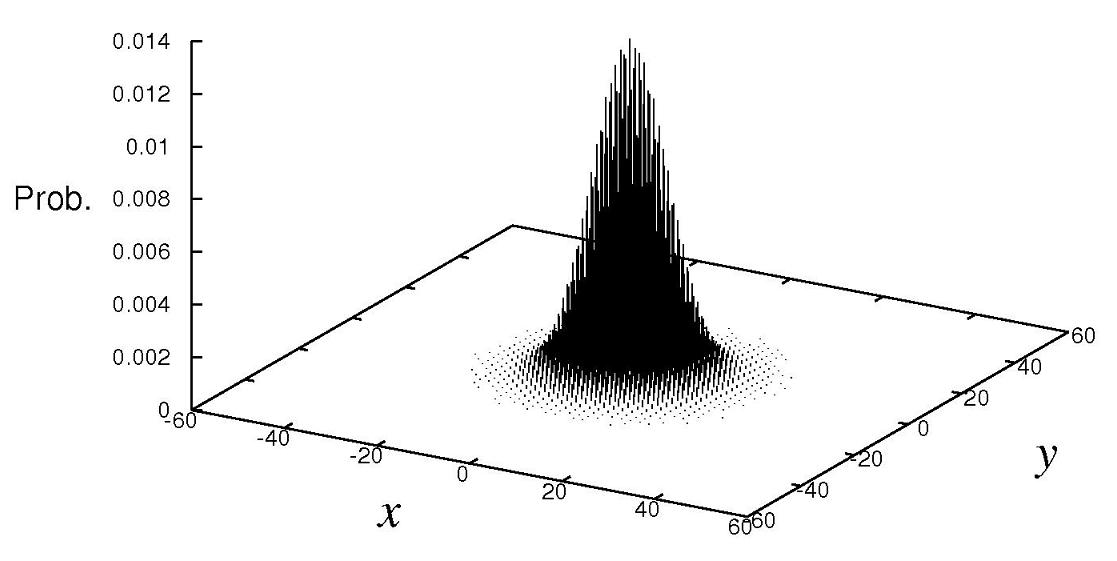 図14 : 2次元ランダムウォークの確率分布
図14 : 2次元ランダムウォークの確率分布
結論から述べると,図だけから少しわかりづらいかもしれませんが,2 次元 4 状態の量子ウォークの場合,図 13 (a) のアダマールウォークと図 13 (b) のフーリエウォークは,線形的拡散を示しますが,局在化が起こりません.一方,図 13 (c) のグローヴァーウォークは,前半で紹介した 1 次元 3 状態グローヴァーウォークと同様に,線形的拡散を示すと同時に,局在化も起こします.
さらに未来へ
量子ウォークでも一般の多次元やグラフの場合は,さらに挙動が複雑なものも存在し,百花繚乱の如き観を呈します.まさにその分類など,リアルタイムで研究が行われている最中です.例えば周期性など,スペクトル写像定理等を用いて,その数学的な解析は進展しています.
今まで紹介したモデルは,実は量子コインが場所に依存しないモデルでしたが,場所に依存するモデルを数学的に解析することは一般に非常に難しくなります.しかし,1 次元格子上でアダマールウォークの量子コインを一カ所だけ変えた“一欠陥モデル (one defect model)”でも局在化が起こりえることを,筆者がはじめて2010年に示しました.
このことは粗くいうと,量子系の場合にはランダムな環境下で局在化が起こりうるアンダーソン局在(実在する物質中の多電子系において、ランダムな不純物が存在する結果、電子の波動関数が局在するという物理現象)とは対極をなすので興味深い結果です.また,一カ所だけ移動する確率 p を変えたそれに対応するランダムウォークでは,局在化は起こりませんので,一欠陥由来の局在化はまさに量子ウォーク特有の性質と言えます.
現在では,一般的な欠陥のある設定での局在化の判定条件について,精緻に調べられています.さらに,空間依存,時間依存,時空間依存の量子ウォークの数学的研究も着実に進んでいるのです.
量子ウォークについては少しずつですが,種々の極限定理や定常測度などを求めることにより,数学的構造が解明されてきています.また,理論的な側面だけでなく,量子ウォークの実現方法のさまざまな提案や応用,例えば,強相関電子系,トポロジカル絶縁体,放射性廃棄物低減,光学,量子テレポーテーション,量子鍵配送,時系列解析,リコメンデーションモデル(インターネット・Webサービスへの応用)なども研究されています.
例えば,放射性廃棄物低減と量子ウォークとの関連は,同位体の分離を量子ウォークの線形的拡散と局在化の性質を用いて効率良く行える点にあります.
また,光学と量子ウォークとの関連は,量子ウォークが波動性と時間発展という 2 つの特性を自然に取り込んでいるモデルであるという点にあります.またさらに,リコメンデーションモデルと量子ウォークとの関連は,商品を推薦する際に量子の重ね合わせの効果をうまく取り入れている点にあります.
先にランダムウォークと投票者モデルとの関係を少し詳しく説明しましたが,量子ウォークとこのような関係にありそうな量子モデルを見つける研究も進行中です.つまり,ある種の双対プロセスが量子ウォークになりえるような量子モデルです.
将来,実用化に耐えうる量子コンピュータが出現した暁には,このような基礎・応用両面の研究が大変役立つと考えられ,「量子ウォークの未来」を夢想すると,大変わくわくしてきます.

参考文献 (日本語で読める本を紹介します)
1)ランダムウォークや投票者モデルなどの確率モデルに関しては,以下の啓蒙書が参考となるでしょう.
[1-1] 香取眞理『複雑系を解く確率モデル』(講談社ブルーバックス,1997) [1-2] 今野紀雄『図解雑学 確率モデル』(ナツメ社,2000) [1-3] 今野紀雄『図解雑学 複雑系(改訂新版)』(ナツメ社,2006)専門書としては,例えば,以下があります.
[1-4] 志賀徳造『ルベーグ積分から確率論』(共立出版,2000) [1-5] 今野紀雄『無限粒子系の科学』(講談社,2008) [1-6] R. B. シナジ『マルコフ連鎖から格子確率モデルへ』(丸善出版,2012)
2)量子ウォークについては下記の専門的な本しかありませんが,興味のある方は挑戦してみて下さい.比較的読みやすいのは,[2-3] でしょう.
[2-1] 今野紀雄『量子ウォークの数理』(産業図書,2008) [2-2] 今野紀雄『量子ウォーク』(森北出版,2014) [2-3] 町田拓也『図で解る量子ウォーク入門』(森北出版,2015) [2-4] 町田拓也『量子ウォーク -基礎と数理-』(裳華房,2018)特に,量子ウォークの最新の動向について知りたい方は,代数・幾何・解析・確率論・応用の各側面から21名の執筆者によって書かれた以下の本が最適です.
[2-5] 今野紀雄, 井手勇介(共編著)『量子ウォークの新展開 -数理構造の深化と応用-』(培風館,2019)本稿の文頭で紹介した,量子超越実験に関しては,以下が参考になると思います.
[2-6] 藤井啓祐『驚異の量子コンピュータ -宇宙最強マシンへの挑戦-』(岩波書店,2019)














