1.はじめに
深層学習の躍進から始まる人工知能ブームが始まって久しい。深層学習は、2012年の画像処理の大会でその存在が広く認知され、その後に様々な分野への応用が推進された。有名な例の一つとして、DeepMind社/Google社による囲碁AIのAlphaGoが、2016年に人間のトッププロを破ったことは象徴的なイベントとして宣伝された[1]。2020年現在の深層学習は、社会インフラや科学技術の探究など多くの領域の基盤を支える技術として、社会の様々な場所に浸透し始めている。この活躍はいろいろな要素の複合の結果ではあるが、その要因を一言で述べるなら、「深層学習は賢い」という経験的事実、つまり既存の技術ではできなかった情報処理を深層学習が行うことができるということがあるだろう。
本稿では、”深層学習はなぜ賢いのか”という一般的な問いに対して、数理的な側面からの議論を行う。ここでは、数理の一つの方法である統計学的な知見を用いて、そもそも学習するとは何かということと、深層学習が賢さを手に入れるとはどういうことかを概観する。その上で、深層学習の特有の構造がどのようにその賢さの獲得に影響しているのか、最近の学説のいくつかを紹介する。
2.深層学習と“賢さ”の定式化
深層学習の定義は無数にあるが、なるべく一般的な回答をするならば、「大量のデータから知識を学習し活用することが可能な計算機上で実現するシステムの一つ」と言えるだろう。同様の役割を持つ計算機システムは数多くあるが、深層学習はその中でも頭ひとつ抜けた性能を発揮するシステムである。すなわち、ここでは”賢い”システムであるとみなす。
話を進める大きな前提として、どういうタイプの”賢さ”を議論したいのかを限定したいと思う。本稿では、”賢さ”の一側面としての数理的な定式化を用いる。ここで”数理的な”という断りのもとで議論の対象を狭めたのは、”賢さ”という多様な理解や解釈が許される概念に対して、分析する側面を絞ることである程度の厳密化を実現させるためである。
本稿で考える数理的・統計的な賢さを、「与えられたデータから、本来は観測できない知識を推論する力」だとしよう。それは、数式を用いて以下のように定義される。具体的な教師あり学習(回帰)を考えよう。今、我々はデータとして$n$個の確率変数の組$(X_1, Y_1), …, (X_n, Y_n)$を観測しているとする。そして、これらの組は以下のような関係性を持っているとする:
$Y_i = ƒ^* (X_i)+\varepsilon_i, i=1, \cdots, n.$
ここで、$ƒ^*$は未知の関数で、$\varepsilon_i$は$X_i$と独立なノイズ項である。例えば以後の例で、$X_i$が盤面で$Y_i$が指すべき手だとすると、関数$ƒ^*$は盤面から次の理想の手を導ける神託のような存在であり、”観測できない知識”である。我々は$ƒ^*$自体を直接知ることはできないが、代わりに観測しているデータからこれを推定できる。ここで、人間が求めた関数を$ \hat{ ƒ } $とし、これが$ƒ^*$にどれだけ近づくことができたかで賢さを評価する。よって、”深層学習が賢い”ということをこの定式化に則って言い換えると、”深層学習によって構成された$ \hat{ ƒ } $は(他の方法に比べて)$ƒ^*$にとても近い”と言い換えることができる。すなわち、二つの関数間の離れ具合を表現する距離$D(⋅,⋅)$を用いて
$D(ƒ^*, \hat{ ƒ } )$
を小さくする$ \hat{ ƒ } $が、”賢い”方法であるといえる。ここでは教師あり学習(回帰)の例を考えたが、類似した設定で分類や教師なし学習を考えることも可能である。
それでは、深層学習はどのように$ \hat{ ƒ } $を構成するのか。深層学習は、多層ニューラルネットワークと呼ばれるモデルを用いて関数をモデリングする。多層ニューラルネットワークは、その名前の通りたくさんの層を持つモデルで、かつ各層はノードと呼ばれる概念で構成されており、それらをつなぎ合わせた様子が神経回路網のようであることからニューラルネットワークと呼ばれている。具体的には、$j$番目の層は入力されたベクトル$z$を
$ƒ_j(z)=σ(A_j z+b_j)$
のように変換する。ここで$A_j$と$b_j$はそれぞれパラメータ行列とパラメータベクトルで、$σ$は活性化関数と呼ばれる所与の非線形変換である。この操作を層の数だけ繰り返すことで、ニューラルネットワークは関数を構成している。また、各層の幅を増やすことで、用いるパラメータの数を柔軟に増やすことができる。そして、この関数のパラメータを、データ上の損失関数を小さくするように選択する。すなわち、$F = \{ ƒ=ƒ_L∘ƒ_{(L-1)}∘⋯∘ƒ_1 \}$を多層ニューラルネットワークで構成される関数の集合として、以下の最適化問題
$\displaystyle \min_{ f \in F} \sum_{i=1}^n (Y_i – ƒ(X_i))^2$
を達成する関数を$ \hat{ ƒ } $として採用する(図1)。この式は、$F$内の$ƒ$を操作して二乗誤差$(Y_i-f(X_i ))^2$の和を最小にする操作を示している。いくつかの拡張はあるが、多くの深層学習は原則この定式化に則っている。
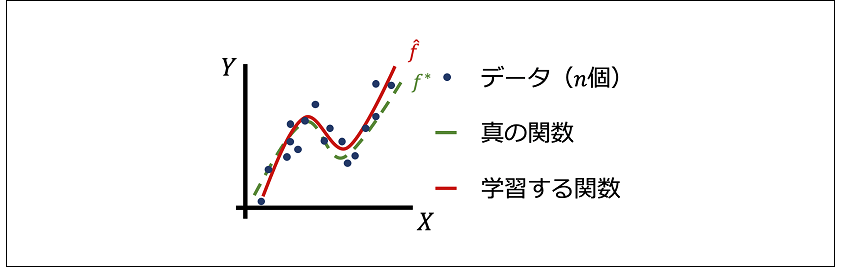 図1:真の関数(緑点線)から生成されるデータ(青点)を元に、学習する関数(赤線)を構成する。
図1:真の関数(緑点線)から生成されるデータ(青点)を元に、学習する関数(赤線)を構成する。
この後の章では、この深層学習による$ \hat{ ƒ } $がなぜ”賢い”のかを議論する。直感的には、真の関数$ƒ^*$という”本質的な知識”を表現するものを、深層学習がいかに精度良く獲得していくのかを紹介する。
3.知識表現の可能性を高める多層構造
深層学習が$ƒ^*$に近づく上でまず重要になるのは、多層ニューラルネットワークが$ƒ^*$に十分近い関数を表現できることである。もし多層ニューラルネットワークのパラメータが非常に少なかったり、活性化関数が適切に選ばれていなかったりすると、$ \hat{ ƒ } $が$ƒ^*$に近づくことはできない。すなわち、実際に最適化問題でパラメータを学習する前に、ニューラルネットワークが十分な表現力、すなわち$ƒ^*$に近い関数を構成するのに必要なパラメータを備えている必要がある。
ここで、ニューラルネットワークの多層構造が大きな役割を果たす。実際のところ、$ƒ^*$それ自体が複雑な形状をしていても、それが簡単な関数の合成で表現できる場合が多い。よって、ニューラルネットワークの各層はその簡単な関数を表現すれば良い。よって、各層ごとに必要なパラメータはごく少量で良い。加えて、それらを足し上げた多層ニューラルネットワーク全体のパラメータ数も、層が1〜2個だけのモデルで複雑な関数を構成する場合よりも減らすことができることが証明されている。すなわち、層を増やすと難しい$ƒ^*$を簡単な要素の集合に分解できるため、モデル全体で必要なパラメータ数も減少するのだ。
具体的な$ƒ^*$を考えてみよう。例えば、$ƒ^*$が図2の下段ような複雑な形状を持つ関数だったとする。これを層の数が少ないモデルで表現しようとすると、階段関数のフーリエ展開のようにたくさんのパラメータを準備して階段を表現する必要がある。しかし層が多いモデルを用いるなら、この関数は簡単な二つの関数の合成に分解することができる。よって、各層は図2の上段ような簡単な関数をそれぞれ構成すれば良い、モデル全体でも少ないパラメータ数さえ準備すれば良い。他の例は、$ƒ^*$が特徴量構造を持っている場合、すなわちより入力データを次元圧縮するような関数の場合である。これは、画像のような見た目次元が大きいデータでは頻繁に現れる性質である。この状況でも、$ƒ^*$を次元圧縮のための関数と出力変数の生成に用いる関数に分解することで、層が多いモデルが少ないパラメータで関数を表現することが可能になる[2]。
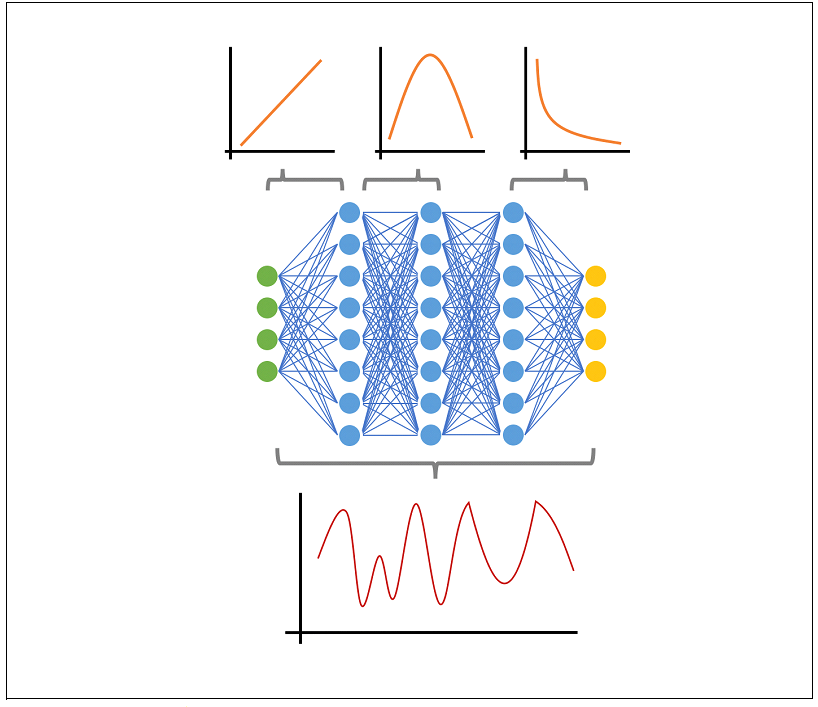 図2:多層ニューラルネットワークと表現する関数の図。各層は簡単な関数を作るが、ネットワーク全体では複雑な関数を構成している。
図2:多層ニューラルネットワークと表現する関数の図。各層は簡単な関数を作るが、ネットワーク全体では複雑な関数を構成している。
この節では、深層学習に用いられる多層ニューラルネットワークが、層の構造を用いてパラメータ数を制約できることを紹介した。すなわち、賢い$ \hat{ ƒ } $を構成するにはある程度の容量を持つモデルを準備する必要があるが、深層学習は層を増やすことで必要な容量を節約できることを指している。すなわち、真に必要な知識$ƒ^*$が非常に高次元・複雑なものであったとしても、層を増やすことでそれを習得できる可能性を高めていると言える。人間の知性に相当するような$ƒ^*$がどの程度複雑なものなのかを測る術はないが、仮にそれが層が少ないモデルでは計算機上で再現できないものだったとしても、この層を増やすという工夫で深層学習がその表現力を獲得している可能性は十分にある。
4.限定的なデータから知識を見抜く学習方法
賢い$ \hat{ ƒ } $を構成するための重要な要素として、与えられたデータの制約に左右されないことがある。$ \hat{ ƒ } $を構成するアルゴリズムは観測されたデータ $(X_1,Y_1), …, (X_n,Y_n)$に依存している。いかなビッグデータがあるとは言え、学習に用いることができるデータが全ての知識を網羅していることはない。例えば、人の顔画像から年齢を予測するようなシステムを作るとき、システムは数十億人の全人類に対して有効な予測を行う必要があるが、その学習に使えるのはたかだか数万〜数十万人分の画像データである。このように、限られたデータから本質的な知識$f^*$を的確に抽出することが重要である。技術的には、観測したデータの情報に左右されずに適切に必要な知識を得られることを、「汎化する」と呼ぶ。
深層学習は、この「汎化する」ことが得意であると知られている。すなわち、学習に用いるデータの不足や偏りなどにあまり左右されずに、欲しい知識$ƒ^*$を非常にうまく発見できる。深層学習が登場する以前の他手法は、この「汎化」に失敗することが度々あり、その現象は「過適合(もしくは過学習)」などと呼ばれていた。すなわち、学習に用いたデータを過剰に信じ込んでしまい、適切な知識の習得ができていない場合である。この過適合は、例えば志望校の過去問しか解けない受験生のようなもので、既存の過去問は完全に分かっていても知識化されていないため、入学試験で出てくる新しい問題は解けない。対して、深層学習は過去問から普遍的な知識を獲得できるため、新しい問題が解けることが知られている。
さらなる前提として「過適合が発生する理由」を押さえておこう。定説では、モデル$F$の自由度が高すぎる場合、すなわちモデル$F$を構成する関数のパラメータの数が多すぎることが過適合を起こすと考えられている。上記の受験生の例で言うなら、記憶力が高すぎる受験生ほど、過去問の解答を丸暗記してしまって新しい問題に正解できない。対して記憶力が高くない受験生は、少ない記憶量でうまく過去問に応えるために普遍的な知識を獲得せざるを得ず、それが逆に新しい問題に正解できることにつながっているというものである。
それでは、なぜ深層学習はこの「汎化」が得意なのだろうか。深層学習で用いられる多層ニューラルネットワークは、一般に膨大なパラメータ数を持つため、定説の考えに則るなら過適合を起こすはずである。しかし、実際の深層学習は汎化を実現するため、定説と矛盾している。現時点でこれを説明する明確な答えは得られていないが、いくつかの仮説が提案されている。
有力な仮説の一つに、「暗黙的正則化」がある(名称にはいくつかのバリエーションがある)。これは、多層ニューラルネットワークモデル$F$のうち、本当に有用な要素はほんの一部で、残りはほとんどが学習の初期段階を除いて使われていないというものである。この学説に則ると、深層学習は巨大なモデルを準備してはいるが、実際にパラメータを学習する際には非常に少ない数のパラメータしか使えないため、それが普遍的な知識の抽出を実現できるという説である。これはいくつかの実験的な研究によって支持されている。例えば図3は、一度学習した$ \hat{ ƒ } $から大半のパラメータを削除しても、関数としての性質は変わらなかった様子を示している。これより、深層学習は実質的には小さな部分モデル$F’ \subset F$ で $ \hat{ ƒ } $を構成しており、使われなかった膨大なパラメータはその学習を初期段階で少し補助するのみなのではないか、という考えが成立する[3,4]。近年は、この仮説に基づいた新しいアルゴリズムなども数多く提案されている。
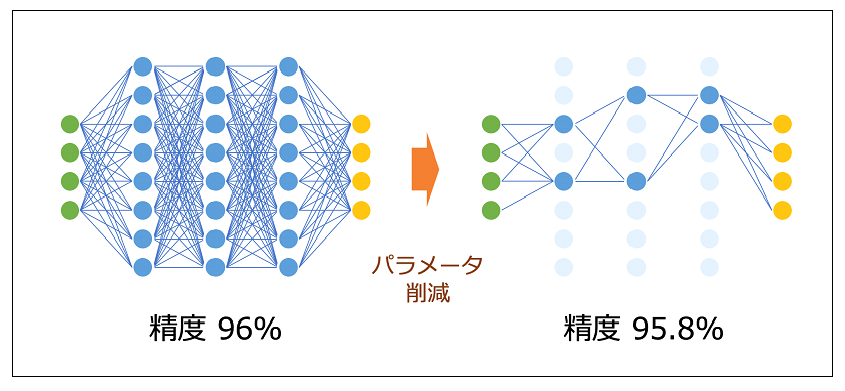 図3:高い精度を発揮するニューラルネットワーク(左)と、そのパラメータの大半を削減したニューラルネットワーク(右)。適切にパラメータを削減すれば、その精度はあまり変動しない。
図3:高い精度を発揮するニューラルネットワーク(左)と、そのパラメータの大半を削減したニューラルネットワーク(右)。適切にパラメータを削減すれば、その精度はあまり変動しない。
直感的にまとめると、深層学習は大きなモデルを使ってはいるが、モデルの不要な部分を切り捨てる構造を持っているため、結果的にデータの偏りに惑わされない知識獲得ができる。この説はまだ議論の段階で精密な理論の確立には至っていないが、今後の発展によって理解がより進展することが期待される。
5.終わりに
本稿では、深層学習の「賢さ」について、特定の側面と定式化を用いて議論した。ここで紹介した仮説は、以下の二つにまとめられる:
A,深層学習は多層モデルを使うことで、複雑な真の知識$ƒ^*$に対しても、計算機上でそれを簡単に表現できる。
B,深層学習のモデル$F$は、そのほんの一部$F’ \subset F$しか使われないため、データの偏りなどに左右されづらい普遍的な知識$ƒ^*$を抽出できる。
以上の仮説に則ることで、深層学習が$ƒ^*$に十分近い$ \hat{ ƒ } $を構成できる概要が朧げに構成できる。もちろん、これらの仮説はまだ発展途上で、実験的な検証や理論的な解釈などは研究が進んでいる途上である。
また、他にも多くの仮説が深層学習の賢さを説明するために提案されている。未だ議論は尽きていないため、今後の研究の発展に注視したい。

【参考文献】
[1] Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G., … & Hassabis, D. (2016). Mastering the Game of Go with Deep Neural Networks and Tree Search. Nature, 529(7587), 484-489.
[2] Imaizumi, M., & Fukumizu, K. (2019). Deep Neural Networks Learn Non-Smooth Functions Effectively. In International Conference on Artificial Intelligence and Statistics. Proceedings of Machine Learning Research (PMLR).
[3] Hinton, G., Vinyals, O., & Dean, J. (2015). Distilling the Knowledge in a Neural Network. arXiv preprint arXiv:1503.02531.
[4] Frankle, J., & Carbin, M. (2019). The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. In International Conference on Learning Representations.