この感染は拡大か収束か：再生産数 R の物理的意味と決定
～単純なモデル方程式に基づく行動変容の判断のために～

印刷用PDF

1. はじめに

2019年末、中国湖北省武漢で発生した新型コロナ肺炎（後にCOVID-19と命名）は、2020年2-3月現在、世界的な猛威を振い[1]、3月12日には、（遅きに失した感もあるが）世界保健機関（WHO）がパンデミック（世界的大流行）を宣言した[2]。

初期の報告で、潜伏期間が平均5日、最大12日と聞き、渡航者も人員交流も多い日本の検閲をくぐり抜け、いずれ入ってくることは多くが予期していたであろう。

中国では初動に遅れ、爆発的な拡大（エピデミック、流行病、疫病）になってしまったが、その後、徹底的な隔離と外出禁止、消毒などの施策により、現在は「現在の患者数（現有確診病例）」が低下している。（当事者には気の毒ではあるが）これは我々の行動のあり方の参考とすべきモデルケースであるといえよう。

実際の人間の行動もウイルスの特性も多種多様であり、（仮にできるとして）それを模擬するには、大規模なシミュレーション（模擬計算）、ビッグデータが必要なのは想像に難くない。しかし、「シミュレーション結果で〇〇だから、ああせよ、こうせよ、」といわれても、なんだか機械に使われているようで得心がいかないのではないだろうか（？）

そこで本稿は、最も単純な疫学の数理モデルに基づく方程式をもちいて、自分がおこなっている、あるいは社会が課している行動規範がどのような意味をもち、要求される行動変容がどの程度の効果をもっているものなのか、理解、納得するための指針となることを目的にまとめた。その点で、本稿は新しい成果や研究ではなく、既存のモデルやデータから読み取れる内容を非専門の筆者から、非専門の読者に伝えることを試みたものである。その中で具体的な値は、実験物理の手法をもちいて決定することが可能であることを示した。

本稿は、指数・対数関数と微分方程式の基本的なところを学んだ高校後半や大学生、疫学を専門とはしない広い範囲の理系の読者を想定した内容にしたつもりである。しかし、そのような基礎知識がなくとも、図やデータを眺めながら7章まで読み進めていただければ、等比級数的に進行するウイルス感染の「見方」「考え方」を深めていただけるのではないかと考えている。

2. SIR モデル（ケルマック・マッケンドリック・モデル ）

人口が一定の「閉じた空間」（実生活の感染リスクとして用いられる「閉鎖空間」でなく、人の出入りを考えないモデル上の領域のこと）での状態が刻々と変わっていく遷移のダイナミクス（時間的な動き）を考えてみる。

状態としては、感受性人口 S （Susceptible： 感染する可能性のある人)　、病例数 I （Infectious： 感染して病気になった人，潜伏期間はここでは無視）、快復数 R （Recovered / Removed： 快復または隔離された人）の3つのみを定め、それらの時間変化を記述する。特に時間tの関数であることを明示するには、それぞれ S(t) 、I(t)、R(t)と書く。

ここでいう「隔離」とは治癒による免疫獲得または死亡であり物理的な隔離ではない。死亡率が比較的低い今のCOVID-19のような場合では死亡率は快復率に繰り込んでよい。全人口N = S(t) + I(t) + R(t) = [一定] であり、転出・転入・この感染以外による死亡は考えない、いわゆる局所モデルである。

このモデルは「ケルマック・マッケンドリック・モデル：Kermack and McKendrick (1927) 」と呼ばれる。同じモデルが変数S・I・Rから「SIRモデル」とも呼ばれる[3]。最も単純化されたモデルであるが、複雑なモデルも、これを基本にした拡張と考えると理解しやすい。非常に汎用的な方程式なので、検索するとかなり詳しい解説もインターネット上で入手できる[4]。

筆者の専門である、プラズマ分光学の分野には奇しくも「コロナモデル」という、原子や分子の状態間遷移のダイナミクスを記述して、太陽コロナの発光強度を求める方程式系がある。「コロナモデル」や「SIRモデル」のような形の方程式（微分方程式、あるいはレート方程式）自体は、様々な分野で使われる一般的なものである。ここではイメージしやすいように、原子のエネルギー準位に見立てた図1の配置で記載することをご容赦いただきたい。

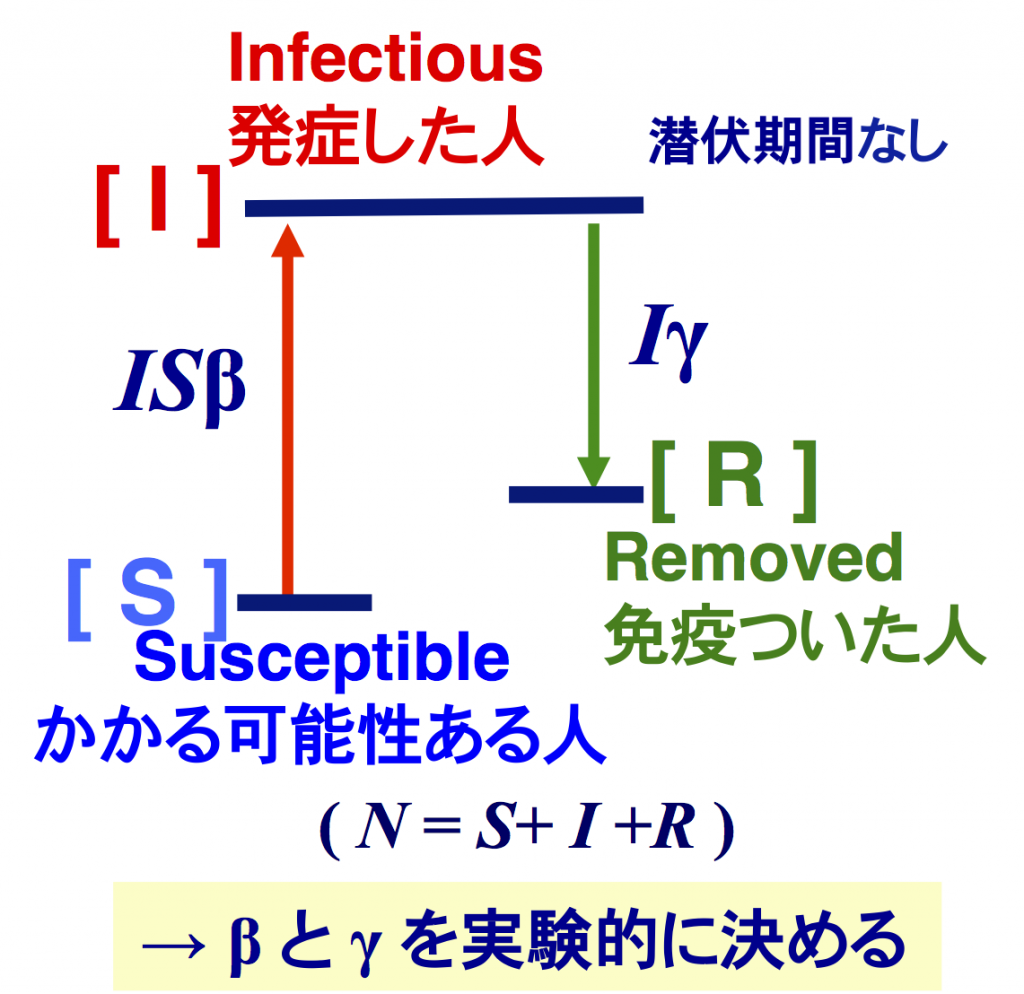図 1：単純モデル（ケルマック・マッケンドリック；SIR モデル）の状態間遷移と速度係数の概念図（原子の励起準位に見立てている）。原子内電子の「励起」（感染・発症）と「脱励起」（快復）の「レート方程式」（微分方程式）の解に対応

本稿で扱う微分方程式では、特に状態[I]への流入と流出に着目する（物理学でいうフラックス；[人s^-1]）。

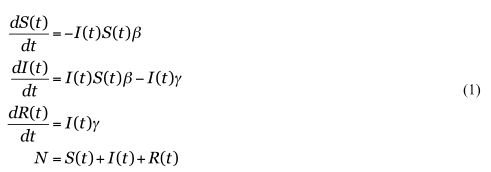
とかける。感染初期でS ≒ Nであれば、2つめの微分方程式は単独に解けて、

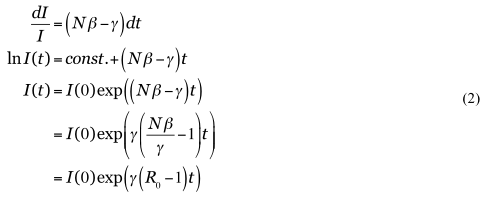
を得る。ただし、

である。

ここで、R₀は基本再生産数（basic reproduction number; R nought, アールノート)といい、ウイルスの感染力の強さの指標として引用される[5]（しばしばその意味、性質が混乱して言及されているように思われる）。感染初期なので、何の対策もしていない場合の値である。

式(2)の指数関数の性質が (R₀ –1) の正負で変わることからわかるように、R₀ < 1なら[I ]は指数関数で減衰するので感染は収束トレンドへ、R₀ > 1 なら指数関数的（等比級数的）に感染が爆発する（感染初期）。

このR₀の中身に着目すると、ある閉じた空間（国だったり、地域だったり、学校だったり、家庭だったり、、）内の人口Nに依存しているので、人口が密集すると大きくなる。同時にこのR₀はβにも依存しているので、感染する機会（行動、生活習慣、文化など；濃厚接触と言われる）にも依存する。よって、発生した場所の状況によって幅があることに注意すべきである。

N < γ/β であれば常にR₀ < 1であるので、感染が拡大する人口密度の臨界値N_crが存在する（、、、がNβの形で扱うので、実用上はあまり有用ではないように思われる）。

3. エピカーブ〜単純モデルと実際〜

SIRモデルの微分方程式を実際に解いたものを 図2に示す。このような曲線をエピカーブ（エピデミック・カーブ、流行曲線）と呼ぶ。

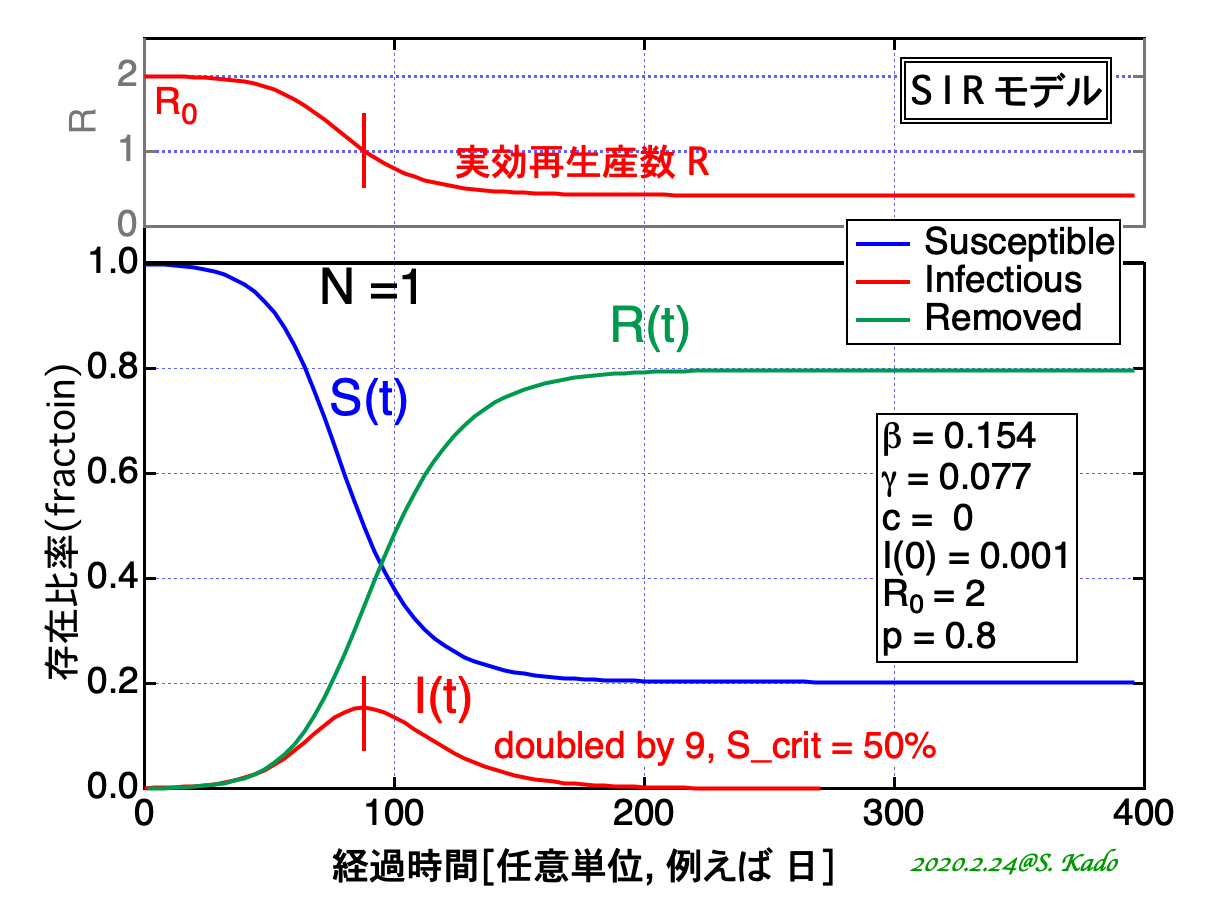図 2：エピカーブの例。縦軸は N に対する S または I または R の割合。初期の感染者 I(0)が N の 0.1%の人数発生し、感染が拡大する。基本再生産数 R0 = 2 を例にした。快復が増え、人々が免疫を獲得すると、この感染が終息に向かう。

係数βとγには、R₀が2となるように適当な数値がいれてある（半減期9）。この例では、[I ]のピーク値で人口の15%ぐらいの人が感染しているような結果になっている。このピーク値は初期値や変数の調整で変更できる（自分でやってみると感覚が確かめられる）。

感染発生からしばらくたつと、快復者（や死亡者）がでてくる（図2中の緑色の曲線）。[S]が[N]ではなくなり、[I ]への流入が減る。[I ]の時間変化は快復者があるのでなだらかになり、[S]が減ることによりやがてピークを迎える。

このときの再生産数Rを、基本再生産数R₀と同様に定義すると

と表せる。これは実効再生産数と言われる（快復数の変数R(t)と混同せぬよう）。さらに、この頃には、政府や個人も対策をとっているであろうから、その効果(efficacy)をc で表すことにしよう（0 < c < 1)。具体的には、ワクチン、手洗い、マスク、検疫や封鎖などさまざまであり、それらを総合的に反映する割合と思っても良い。したがって、

と書くのを推奨したい。こうすれば、風習を変えること（専門家会議[6]のいう「市民の行動変容」）によるβの低減率も(1-c)に含まれると考えられるからである。

図 2 とは別のパラメータ（βとγの別の値）および初期感染者数 I(0)を用い、ピークを 30％程度にあわせた場合の、c の値への依存性を図 3 に示す。

アウトブレイク後に医療体制を整えて許容数を増やしていくイメージを、図 3に加筆した（図3の赤点線）。有効な予防策や行動変容(c = 30%, 50%)を実施すると「ピークを遅らし、下げることによって、医療崩壊を防ぐ」ことができる、という意味がつかめるであろう。

専門家会議[6] では感染者の指数関数的な増加により医療体制の許容量を超えることをオーバーシュートと呼び(3月19日)、その後「2〜3日で累積患者数が倍増する程度のスピードが継続して認められるもの」と再定義（4月1日）した。オーバーシュートは物理学や工学の分野では、過渡応答などで、ある基準を行き過ぎてしまう現象を指すのが一般的である（逆はアンダーシュート）。色々な物理量の速すぎる増加は「サージ」を用いることが多いように思う（サージ電流など）。疫学の専門誌でも「最初に感染を抑えすぎて集団免疫が不足で、アウトブレイクの第2波がきて、結果として最適な免疫獲得よりも行き過ぎた感染者を出してしまう状況」を指してovershootとする例[6 補足]があるため、限定的な用法であることに注意しておくべきであろう。感染症流行時の医療体制の過渡的な容量のことはsurge capacityと言われる。医療従事者に感染が広がると、この容量が増やせずに医療崩壊のリスクが高まる。

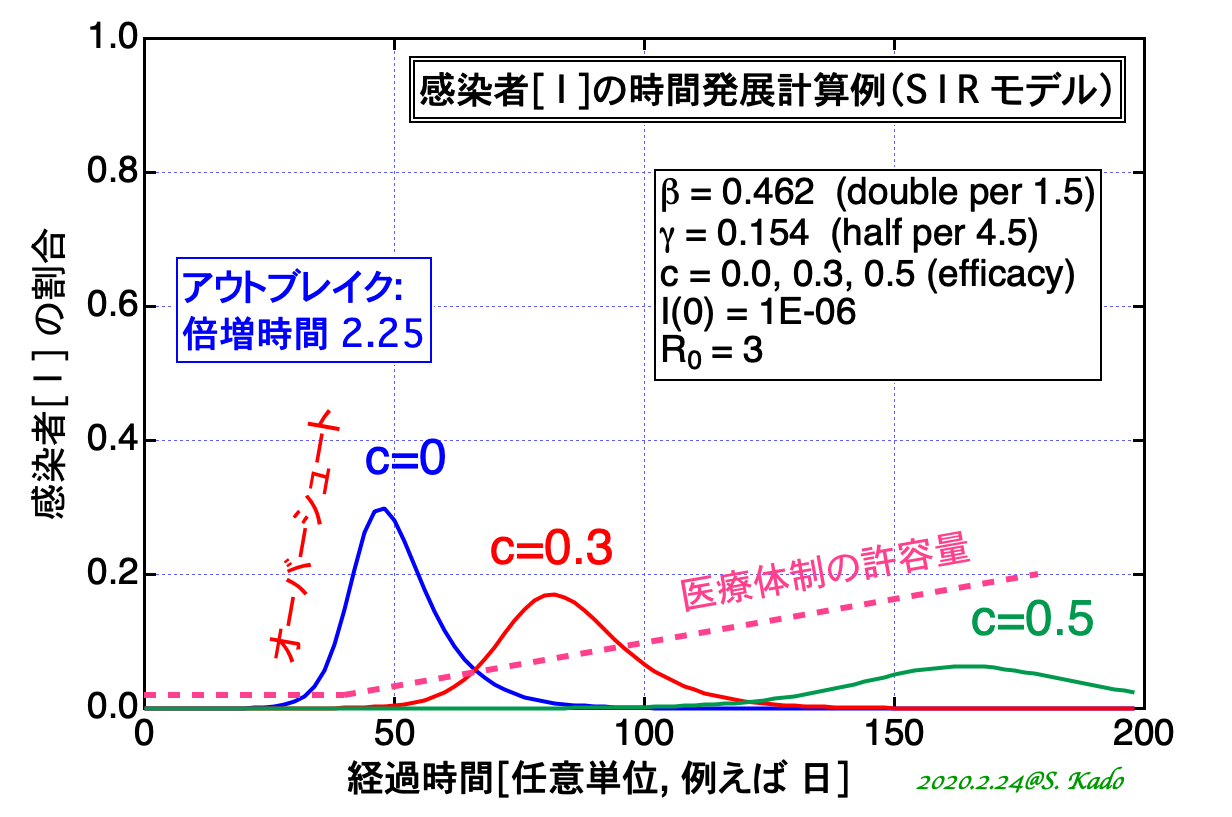図 3：感染者動向の予防効果率 c への依存性。R0 = 3、半減期 4.5 、初期感染者 100 万人に 1 人を仮定。予防効果（c の値）が増えると、ピークの到来が遅れ、ピーク値が下がることがわかる。ただし、終息（集団免疫を獲得する）には時間がかかる。アウトブレイク時の現有感染者の倍増時間は時定数の逆数の差の逆数 (1/1.5 – 1/4.5)^-1 = 2.25 で表せる。

S/Nは抗体非獲得率ともいえ、多くの人が感染して抗体をもつと[S]が小さくなる。たとえば麻疹や風疹などのように終生免疫を持つ人が増えれば[S]が小さくなり実効再生産数Rが下がる。ワクチン摂取率がcであれば、Rをさらに(1-c)倍にすることができる。これを集団免疫という。

感染初期で抗体をもつ人がさほどいなく、ワクチンも完成していなければ[S]の低下（集団免疫）は期待できない。このため[S]がほぼ[N]で一定のままエピカーブが進展すると解釈してもよい。

＜指数関数・対数関数の時定数＞

指数関数の時定数は関数がe倍、または1/e倍になる時間である。実用上は時定数を、倍増、半値に変換できるようにしておくと便利である（e = 2.71828… は自然対数の底、ネイピア数でln(e) = 1である）。それには高校数学の対数関数の底の変換公式を用いて（もちろん導出もできる） 、式(6)

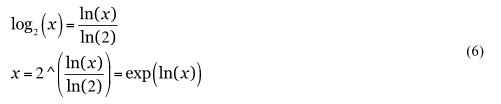
から求まる。

ln(x) = t/τとおくと

を得る。τ > 0なら増大、τ < 0なら減衰である。関数値が一定のままであれば時定数τは無限大である。ln(2) = 0.69… なので、半減期=減衰の時定数τ× 0.69、増倍時間＝増大の時定数τ× 0.69である（関数は同じでも、時間軸の目盛りの切り方が、「時定数」ごとに1/e倍またはe倍から、「半減期」ごとに1/2倍、または「増倍時間」ごとに2倍にかわると考えると理解しやすい）。

4. 基本再生産数 R0 の実用的な求め方（仮称：半減期法）

筆者を含む物理学者は、感染の疫学やウイルス学の詳細を知らない、いわゆる非専門家ではある。しかし実験物理学の方法をもちいて上記のような微分方程式の係数を決定することは、頻繁に行っている。むしろ、先入観を排することによる知見も意味があるかもしれない。

たとえば、基本再生産数R₀の値はこれまでのインフルエンザや麻疹の値が引用されるが、上述のように[N]やβ、すなわち集団の規模や習慣によって全く異なることもあり得る。

ではどうすればR₀を求めることができるだろうか。本稿では2章に述べた単純モデルに従うが、限られた情報から初期的な評価を行う場合には、このモデルを基本とするのが妥当だろう。設定条件が複雑になればなるほど、「イメージ」をつかむのが難しくなることも想像に難くない。ただし、係数の物理的意味を逸脱するような仮定には慎重にならなければならない。

初期（S ≒ Nの時期）における[Nβ]は、[I ]が与えられた時のdS/dt の変化率（減少率）である（式(1)の第1式を参照）。[I]が増えると、その分[S]が減る。よって[I]の発生を数え上げて（発症者の積算数）いけば、それは[S]の減少をみていることになる。

クラスターの発生は[S]の減少を仮定しないので、ある時点t₀からtまでの発症者の積算数（累計数）[J]は、

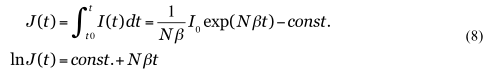
のように表せる。従って、発症者の積算数あるいは累計数（式(8)）の対数グラフの直線部分の傾きから、時定数1/Nβを求めることができる。同様に、施策や行動変容を含めた実効的な時定数は(Nβ (1-c))^-1とかける。

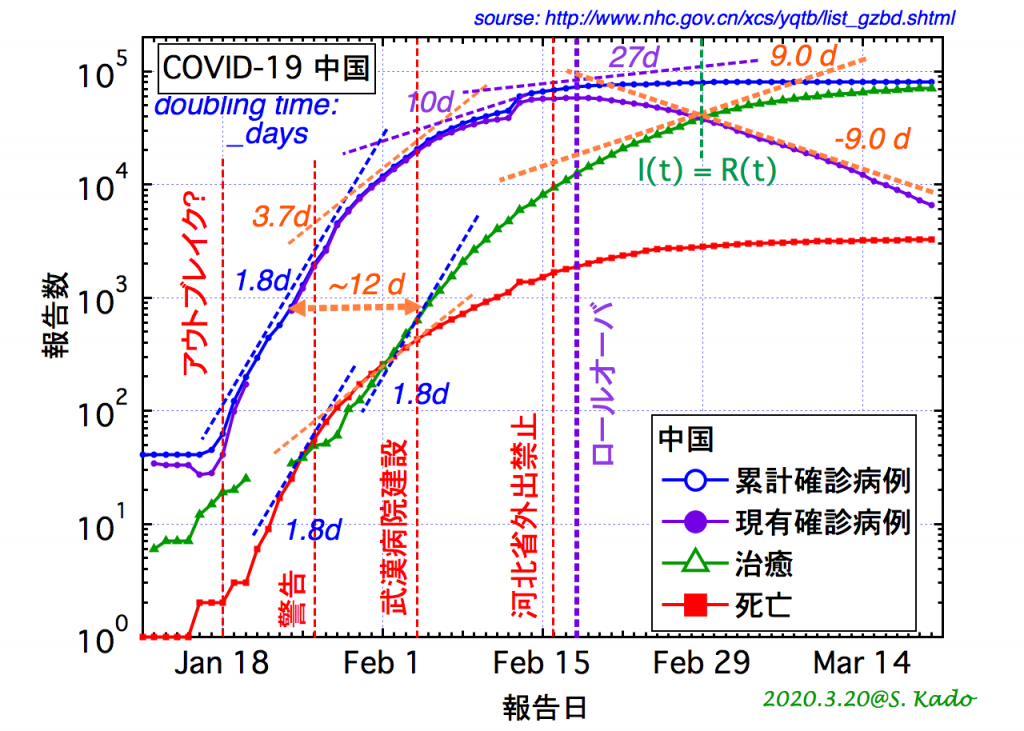図 4：中国における COVID-19 の感染動向[7]を示す片対数グラフ。直線部分の傾きの逆数から時定数（ここでは倍増時間; doubling time に換算）がわかる。

中国におけるCOVID-19の発症者および快復・死亡者のエピカーブを図4に示す。データ[7]は、感染初期(1月22〜28日)では1.8日毎に累計病例が倍増している。

式(6)の換算を用いて、累計症例の時定数τ_J = (1/Nβ) = 1.8/0.69 = 2.6 を得る。これでR₀ の分子Nβが得られた。

次はR₀の分母γである。これは快復率なので、感染初期から求めることができない。その後の中国では、[I]の累計数の増加率が倍増時間で3.7日、さらに10日へと順調に減り、快復者も増えてきた。[I]への流入が小さくなり、[I]からの流出が大きくなると、時間変化はほとんど快復率で記述できる。このため、対数グラフに直線部分が現れれば、それが時定数となる。快復数[R]の増加も同等であるが、現有数[I]が増加から減少へと転じるロールオーバ付近（2月17日前後）では、[R]の直線部分の特定はまだはっきりしていなかった。

もちろん、式(1)の第3式

から、快復数（+死亡数であるが影響は無視できる）[R]の時間微分をとって、I(t)で割ればγが出る。しかし、単純モデルに比べると時間遅れや対数グラフの利点が活かせないなどを気にすると、その時点ではあまり乗り気がしなかった（自信がなかった、というべきか）。結果として振り返ると、R = Iとなる時間（2月29日）における対数グラフの傾きはどちらもほぼ同じであるので、快復期であれば近い値を与えそうである。

すなわち、この時点（2月29日）以降では、[I]への流入が抑えられているので、現有の[I]の時間変化は快復数[R]への流出とバランスする。よって、両者が同程度の9日で、倍増、半減する。この半減期を時定数(1/γ)に換算すればγを求められ、目的の基本再生産数R₀ の評価が可能となった。

半減期を直接求め、それ以前にさかのぼってR₀を求め、その後の時間変化であるRを追う方針を特徴づける意味で、これを仮に「半減期法」と呼称したい。この方法は、後に述べる「（仮称）発生間隔計数法」や「（仮称）ロールオーバ法」に比べ信頼度が高いが、現在進行中のエピデミック（この場合は中国）の施策評価にリアルタイムで反映するのは難しい。半減期を用いる利点は、国際比較における判定基準の差異にかかわらず、それぞれの国内で類似した基準で判断されていれば、現有感染者が減っていく時定数は同じと見なせるところである。

5. 各国の再生産数R₀およびRの値と予防の効果

再生産数（R₀およびR）の物理的な意味は、「ある一人の患者が人口Nの「閉じた空間」に入ったとき、その感染可能な期間において何人に感染させるか」である。

累計数の倍増時間(doubling time, 倍加時間)と半減期(half decay time)を用いる（上記のような）「（仮称）半減期法」は、この解釈と親和性がよい。あるクラスターの1人の患者が倍増時間のうちに2人になる、つまり1人に感染させる。そのとき別のクラスターにいた2人の患者の半分、すなわち1人が快復する。このとき再生産数R = 1である。

より厳密には、指数関数では、快復時間の(R-1)倍の割合で指数関数的に感染が広がると考えると理解しやすい。

先例がないと半減期が出ないが、中国のデータで9日を得ている。重症化率や死亡率、発症率などは集団規模や生活習慣によって異なるが、治療法がない時点での自然治癒率はさほど集団によっても差がないと思ってよいのではないか、と考え、採用した。

時定数（半減期）の比を用いる方法（上記4章の「（仮称）半減期法」）は、分子、分母とも同じファクター（k倍、k分の1になる時間）をつかえば、半減期なのか、時定数なのか、の換算は気にしなくてよい。よって、中国における基本再生産数R₀ (@中国)

を得る。やはり感染力が強いことがわかる。

欧州のデータでは、アウトブレイク初期において、連日25-35%程度の割合で増加している。これを倍増時間に変換すると、欧州における基本再生産数R₀ (@欧州) = 3.1~ 2.3を得る。これが（なにもしなかったときの）初期の値であろう。R₀ 単位で予測すると、R₀ = 3であれば9日毎に症例数が4倍になるので、3半減期経った27日後には2^(3-1)×3 = 64倍になり、瞬く間に医療の許容量を超えてしまう。

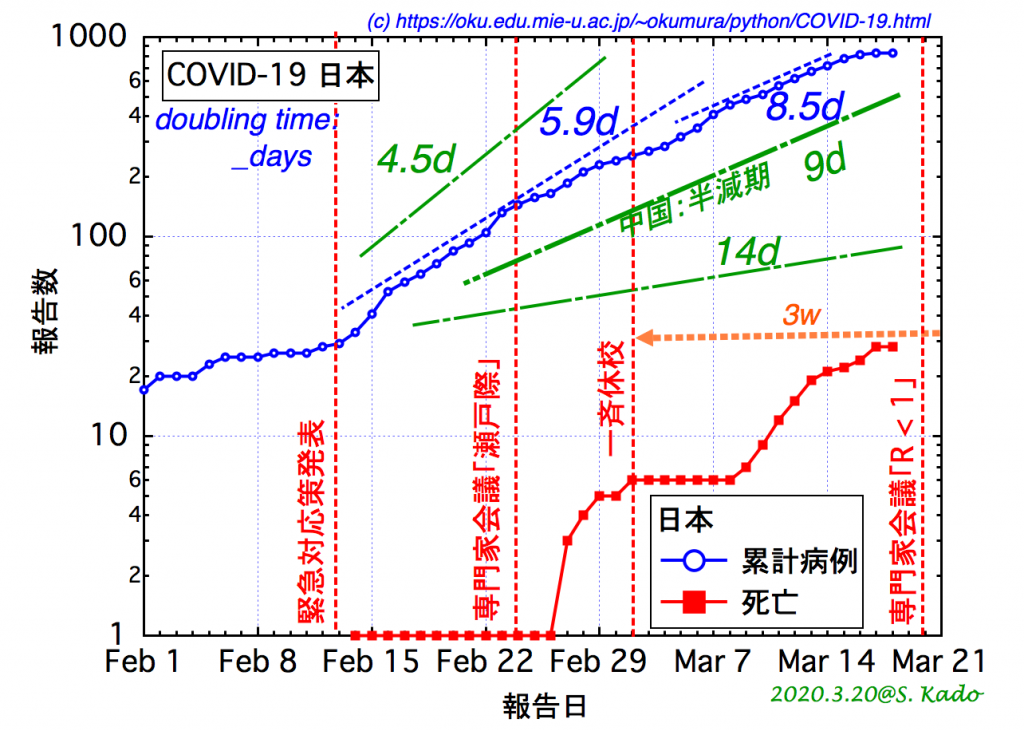図 5：日本における累計の症例報告の時間的推移。中国の現有患者半減期 9 日を用いると、累計病例の倍増時間を 9 日よりも小さくすると R < 1 を達成し、収束へ向かうと推定できる。

一方、図5に示した日本では、2月中旬は累計の症例数が倍増時間5.9日で増加していた[8]。このとき、日本における基本再生産数R₀ (@日本)

である。中国や欧州におけるR₀に比べ、有意に小さい。おそらく、それまでに、中国のデータやクルーズ船[9]の状況をみて、国民の危機意識が高まってきた効果が大きいと思う。指数関数のトレンド（等比級数的拡大）に乗っているので、一部で噂されている、検査数制限による、いわゆる隠蔽的な状況ではないことが予想されたし、その後のトレンド、死亡数のアウトブレイクがはっきりしないことにも矛盾しない。それでも、その割合で増加すると、27日後には2^(1.5-1)×3 = 2.8倍になる（治癒者は除いた現有病例である）。等比級数的拡大は侮れないことがわかる。

3月に入り、さらに倍増時間がゆるやかになり、本稿執筆のきっかけとなった3月15日時点までの累計病例の倍増時間に約8.5日を用いると

に下がっていることがわかる。

これは専門家会議の評価[6]などにもとづき、イベント自粛や全国を通じて学校の休校措置などがなされたり、国民の予防意識がさらに高まったことによると解釈できる[10]。その効果率cは31%である。つまり、様々な犠牲と努力により、3割の予防効果を発揮したと言えるであろう。

結局、累計発症者数の倍増時間を、快復の半減期である9日よりも、緩やかにすれば、R < 1となり、その後、終息（収束）に向かうことが示唆される。これは日々の増加率8%に相当する（1.08の9乗 ~ 2 ）。1週間で約1.7倍である。

2020年3月19日の専門家会議の会見[6]によると、概ねR < 1に抑えられているとする見解であり、本稿の評価とは（評価方法は異なるであろうが）ほぼ同様の見解に思える。

前日までの症例が大きくなればなるほど、新規の発症数（や死亡者数）も大きくなるのはこの方程式からも当然である。報道等では新規患者がどんどん増えていることが強調されがちであるが、何%の増加率かに着目して注視されたい。

6. 対数グラフの有用性

対数グラフの便利さは以下にある 。

1) 微分方程式の係数は敷居が高いが、半減期や倍増時間ならイメージがしやすい。

2) 1桁減/増からも、グラフに物差しをあてて時間幅から、同じ結果が得られる。

例えば、図5において、対策後の実効再生産数Rは快復の1桁減と日本の1桁増の読み取り値から、30/28=1.07であることがわかる。（半減/倍増から9.0/8.5=1.06）

仮に２つのクラスターが現有の感染者I(t)において支配的だった場合は、aを定数として、

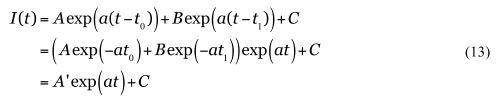
なので、定数Cが小さければ

である。

同じ増加率であれば、発生時期が異なっていても、対数グラフの傾きには影響ないが、定数Cが大きくなれば、誤差になり得る。これは例えば、いったん一つのクラスターが終息（収束）して、累計値が落ち着いた後、さらに別のクラスター発生により上昇を始めるような場合が想定される。その場合は、収束部分を定数（オフセット）として累計値から差し引いた後、対数をとることで回避できる。

快復時間と（本来の定義での）感染性時間を等価と考えてよいか、という疑問もあるだろう。仮に快復時間と感染性時間に時間差があったとしても、指数関数の減衰時間は、基礎方程式(1)に従っているγであるので、むしろ、減衰時間を快復時間と呼ぶのか、感染性時間と呼ぶのか、と解釈するのが適切であろう。

実用面に目を向けると、厳密には感染(検査で陽性)と発症(症状有り)とは異なる。無症状の人は検査にでてこない可能性があり、タイムラグ（潜伏期間と検査のタイミングによる誤差や不顕性感染）もあるので、症状の出た人を数えていくほうが好ましい。ただし、発症率等が一定であれば、対数グラフの傾きは変わらないので、ある程度の期間平均すると、タイムラグの影響は小さくなっていくことが期待できる。

7. 実効再生産数 R < 1 を目指すために

これまでの章で見てきたことから考えると、結局、実効再生産数R < 1を目指すためには、

の各係数を見ながら、以下のような施策、行動変容をとる必要がある、という方針に得心がいくのではないだろうか（ここでχは免疫非獲得率）。

どの対策にも、経済や行動制限などの代償が伴う。

これは、放射線防護で使われるALARA (As Low As Reasonably Achievable) の原則[11]と同様、「社会的・経済的要因を考慮に入れながら合理的に達成できる限り」密集を少なく保ち、かつ各自の防護対策に留意し、快復者の時定数よりも緩やかな累計症例報告数となるようコントロールすることが肝要と思える (with a growth rate as low as reasonably achievable; ALARA)。

この場合の目標値は、「クラスター毎に累計症例の倍増時間が9日よりも緩やか」である。

8. 基本再生産数R₀を求める他の方法：別法1〜（仮称）発生間隔計数法

基本再生産数R₀の定義の元となる式(2)より、I(t)の時間変化は

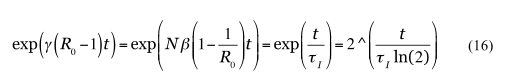
と変形できる(^は累乗を表す)。ここで式(7)の時定数変換式を使った。よってI(t)の時間変化（時定数τ_I）と、Nかγのどちらかが決定できればR₀を求めることができる。

感染拡大初期においてはγが不明であろうから、感染者・被感染者のペアを追跡し、感染伝達の高度なモデリングと統計処理を用いて係数を推定する。感染動態のモデリングにおいては、発生間隔（serial interval）を特定することが重要な課題となっている。そこで本稿ではこの方法を「（仮称）発生間隔計数法」とよぶ。

発生間隔は「１次感染者が２次感染を引き起こすまでの時間間隔」と説明される。ここで、筆者もこの誤解をしてしまったのだが、SIRモデルによる発生間隔は初期の発生頻度を表す係数[1/Nβ]ではない。世代間隔（generation interval）と言い換えられることもあるようで、平均的にはγに近い物理量に対応する。

単純なSIRモデルよりも進んだ、潜伏期間などを入れたSEIRモデル（E: Exposed; 潜伏期間中）などを用いて評価されたりしているが、その分、推定すべき微分方程式の係数が増えてしまう。統計的な信頼度を上げるために、モンテカルロ計算やベイズ統計などの統計処理を用い、確率密度や潜伏期間に相当する時間遅れを推定することになる。どの手法で発生間隔を求めたかが比較の争点になり、それ自体が重要な研究テーマになっているため、詳細は専門家の方々による他所に譲りたい（学術雑誌であるが[12]のような報告もある）。

いくつかの報告を調べると、たとえば、SARS（2003年に報告されたコロナウイルスによる重症急性呼吸器症候群; Severe Acute Respiratory Syndrome）の発生間隔を仮定して、COVID-19のR₀を推定したものなどが目についた

誤解例を１つ示したい[13]（これは[12]の比較リストにも含まれるものである）。

仮に、物理学における衝突周期との類推で、

・患者数の倍増時間7.4日を　 τ_I = (Nβ-γ)^-1×0.69
・患者の発生頻度平均7.5日（SARSのもの）を　(Nβ)^-1

と対応させてしまうと、

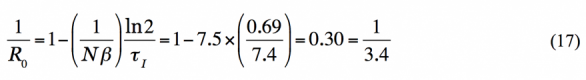
であり、その後の感染拡大を表さない。というより、そもそも、アウトブレイク直後の中国での倍増時間 1.8 日を採用すると、負の値になってしまう。単純モデルによる（非専門家の）「直感」「イメージ」とその分野の係数定義の対応関係を定量的に取り扱うには、やや敷居が高いとも言える。

一方、発生頻度を初期の発生間隔を用いず、快復の半減期 9 を用いることができたとすると、 R0の定義を式変形し

を得る。こちらの場合は、快復時間の時間差が SIR モデルには含まれないため、現有患者数の増加率と累計数の増加率はほぼ等しく、単純な評価では R0を 1 だけ過大評価してしまう。

このように、発生初期のデータとモデリングから詳細に推定をおこなおうとする場合、発生間隔などの物理量の定義を定量的に確認して、SIR モデルの係数と対応するのかどうかを、慎重に確認することが必要であろう。（ここは専門家の方々の評価に譲りたい）。この手法の利点は、感染者の発生をリアルタイムに追跡するため、実効再生産数 R の時間変化（あくまで一定期間過去の統計平均）の鋭敏な推定、特異な感染形態（いわゆるスーパースプレッダー）の存在特定等にも適用可能なことであろう。

ただし、感染者・被感染者のペアを追跡するのが困難な場合もあり、その数が少ない段階では、精度が極端に落ちてしまうこともあるであろう。

9. 基本再生産数 R0を求める他の方法：別法２〜（仮称）時間差法

筆者は初期においては1/γに相当する「感染可能時間」として、中国のデータで快復者が、感染者と同じ倍増時間1.8日で、同じ人数で増加していくあたりの時間差である12日に着目した。これを「（仮称）時間差法」と呼ぶ。ある日発症した人が、平均すると、12日後に退院したことを意味すると想定したためである。潜伏期間や発病から入院までの時間も（ざっくり）加味して安全側に14日を仮定していた。今思えば、快復から退院までも数日あると考え、12日程度が妥当だったかと思っている。

倍増時間14日に相当するγの時定数は　14/0.69 = 20 日である。R0は、分子、分母とも倍増、半減期を用いて R₀ = 14/1.8 = 7.8 となり、これが本当ならとてつもなく感染力の強いウイルスとなる（麻疹(12~18)ほどではないが、風疹(5~7)や天然痘(5~7)並み [5]）。

これもあくまで、感染拡大初期の仮評価と捉えるほうがよいと思える。

10. R0を求める他の方法：別法３〜（仮称）ロールオーバ法

R₀を求めるもう一つの方法として、もう少し[I]の時間的動向が緩やかになったころに（もし採用するならば）適用できる方法が思いつく。本稿では「（仮称）ロールオーバ法」と呼ぶ。

SIRモデル計算例の図2をみると、時間単位42のところで、I(42) の微分係数が0となっている。このときのRの計算値は1を横切っていることが確認できる。快復の半減期を求めた後は、半減期法と同等の扱いで、さかのぼってR0を求め、その後のRを追跡することができる。

図4に示した中国では2月17日頃を境にして、増加と減少が入れ替わる、いわゆるロールオーバ（あるいはピークアウト）と言われる状況に達した。このときdI/dt = 0であるので、微分方程式からはまだN ≒ Sと考えると、実効再生産数R = 1である。この時点でNβ = γであるので、[I]の累計数（式(8)における[J]）の対数の傾きの逆数をγの時定数とみなすことができる。

残念なことに、この付近で武漢の統計方法が修正され、データが不連続となっていて、傾きが出せない。概ね10–17日に収まるのでは？という程度で、「（仮称）時間差法」での感染可能時間(12–14日)でも大きな矛盾はなさそうだ、という感触であった。ただし、図5の日本の規模では、件数が少なく、地域やクラスターを含む、統計的なバラツキが大きいので、この方法は適さない。

この方法は、半減期を直接求める方法よりも若干早く評価をすることができる。しかし、もともとピーク日の決定や傾きの評価、快復と退院の時間差は不確実である。加えて、そのころは累計病例数の増加率も変化しやすいところでもある。従ってこの方法「（仮称）ロールオーバ法」は「（仮称）半減期法」に比べると精度は落ちる。

11. 詳細な感染モデル

本稿では最も単純な感染モデル（「ケルマック・マッケンドリック・モデル」あるいは「SIRモデル」）を用いた。これは今現在の状況と、今現在とれる施策の提案・評価には有用であると思っている。しかし実際、長期的動向の予測を行うには、様々な要素を加えなければならない。その一例を図1と同様な原子の輻射過程に類似した準位図で図6に示す。

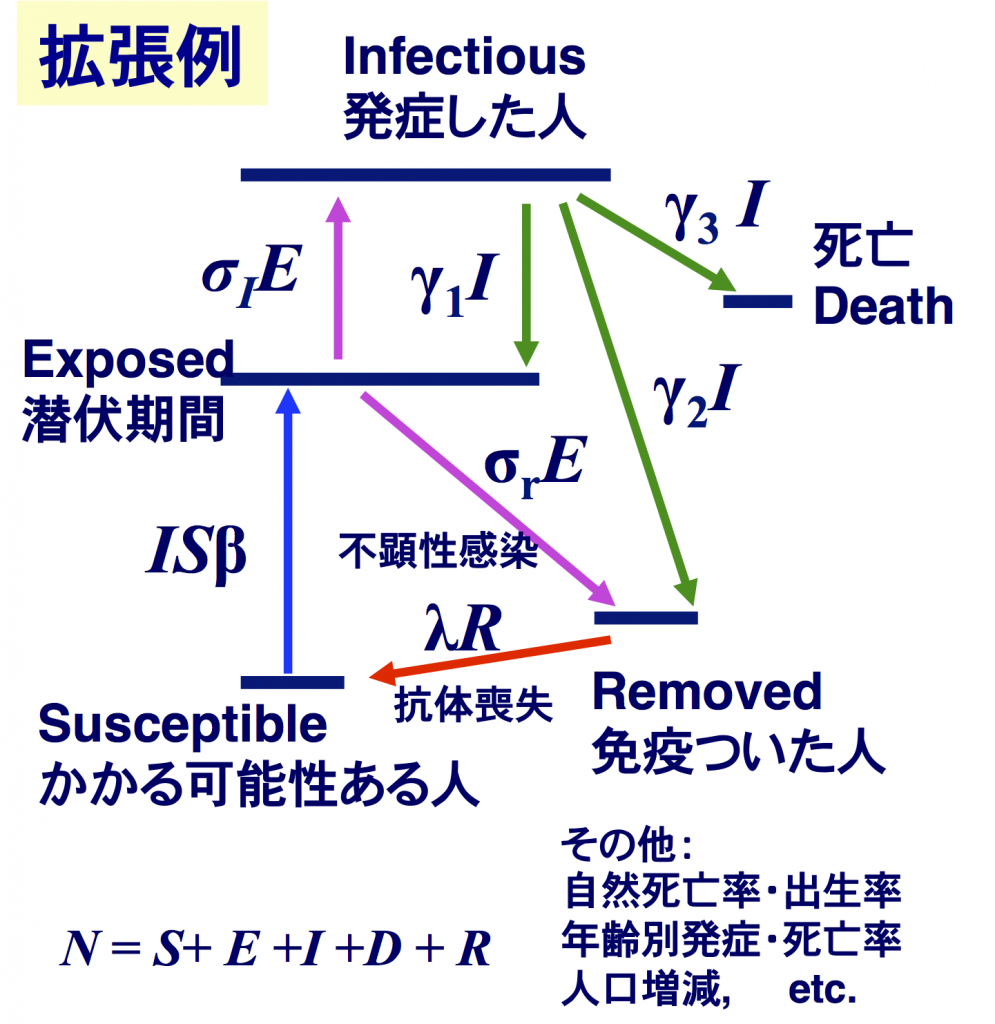図6：様々な状態と速度係数を追加したモデル例。[I]からの流出先は３通り、[E]からの行き先は2通りあり、その係数比は物理学分野では「分岐比(branching ratio)」といわれる。放射線防護や薬物の人体内の移動過程をあらわす目的にも、同じようなモデルがもちいられる（コンパートメントモデル）。

これを解くには、プラズマ分光学の分野で、コロナモデルを一般化した、衝突輻射モデルというものが使われる。各人口への流入・流出を表すレート方程式（微分方程式の連立方程式系）は、以下のような行列方程式の形にかけることが気づくだろう。

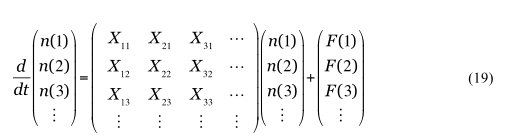
ここで行列要素X_nmの対角成分X_pp は状態pからの流出、非対角成分は状態間の遷移。後ろの項F(p)は人口動態に相当する。通常、原子過程の場合F(p)の項は、再結合により別の電離状態から束縛準位へと流入してくる成分を表す。疫学モデルであれば、死亡率や出生率など、ある状態の密度に対する割合ではなく、一定人数が別の「閉じた空間」と行き来する動きに相当する。それを無視すれば、この微分方程式の連立方程式は行列の対角化により容易に解ける。

さらに、例えば年齢によって係数が異なるような場合には、行列の次元を増やすことにより、拡張することができる。

ただし、それぞれの行列要素を、物理的に意味ある値の範疇で決定するのは必ずしも容易ではない。

12. まとめ

本稿では、一般人（非専門家）が入手可能な情報を用いて、i) 感染の特性、 ii) 施策、行動の指針に対し、自身や家族ができるかぎり納得しうる「物差し」を実験物理学の立場から提供することを試みた。重要な物理量は、基本再生産数R0、実効再生産数R、であり、それを算出する係数としては、累計症例数の増加率（倍増時間）、新規症例が減少した後の現有症例の半減期、現有症例ピーク時の累計症例の増加率である。

手法をまとめると、1) 半減期がわからない場合、2)半減期が求められる場合に大別されるであろう。

これらの係数には手法による違いや、誤差も含まれるので、絶対値は目安と考え、施策や予防によるその経時変化を注視しつつ行動を見つめ直すことが肝要に思える。

多くの方法があって戸惑うが、実際、手法の精度や適用可能性、結果を比較、評価するのも重要な学術研究に位置づけられる。

理系の大学生以上であれば、現実の動態を簡易化（モデル化）して記述する微分方程式の考え方を学ぶよい題材となるであろうし、対数関数を学ぶ高校生にも、グラフの読み取り方、数学の知識が活かされる具体例を学ぶ場となることを願う。

その観点で、文献も筆者を含む非専門の読者が入手しやすい、webに公開されているものを中心に挙げた。当然、より精密な評価は、疫学の専門誌や学術雑誌、いわゆる専門家の方々の解析結果が優先されるべきことに留意すべきである。本稿で紹介した実験物理学的な手法は、単純なモデルをもとに政府発表や報道内容、研究機関からの発表や提言[14]を理解する「見方」の一例を提供するものとして若干でも有用となれば幸いである。

謝辞

SNSへの投稿(@plasmankado)をきっかけに、本稿の執筆の機会をくださいました京都女子大学の水野義之名誉教授(@y_mizuno)に感謝いたします。また、日本国内の感染者データを早期よりまとめていただいておりました三重大学の奥村晴彦名誉教授(@h_okumura)のデータを使わせていただきました。ここに感謝いたします。

—

参考文献・サイト：　　　　　　

[6]厚生労働省：（リンクが変わることがあるので要注意）

– 新型コロナウイルス感染症について：(2020.3.18閲覧) https://mhlw.go.jp/stf/seisakunitsuite/bunya/0000164708_00001.html

– 新型コロナウイルス感染症対策専門家会議の見解等（2020年3月19日）：(2020.3.21閲覧) https://mhlw.go.jp/stf/seisakunitsuite/bunya/0000121431_00093.html

– 新型コロナウイルス感染症対策の状況分析・提言（2020年4月1日）：(2020.4.4閲覧)（同上のURL）

– [補足]疫学専門誌でのオーバーシュート https://royalsocietypublishing.org/doi/10.1098/rspb.2006.0015

本ページの下部には他の有用なまとめサイトが掲載されており、有名な感染者マップも含まれる。
https://jagjapan.maps.arcgis.com/apps/opsdashboard/index.html#/641eba7fef234a47880e1e1dc4de85ce

（2020年3月19日投稿、3月27日公開; rev.2︓4月5日)