目次
1. はじめに
2. 感染症モデルの概略 I「SIRモデル」
2-1) 本稿で扱う「感染症モデル」の概略
2-2) 「単純なSIRモデル」の限界と注意点
3. 電子回路シミュレータ
3-1) LTspice
3-2) アナログコンピュータ
3-3) アナログコンピュータの構成要素
4. 簡単な例 〜運動方程式を解く〜
5. SIRモデルへの適用
5-1) 物理量との対応条件の設定
5-2) S(t)を解くアナログコンピュータの構築
5-3) 行動変容の組み込み
6. 「その1」まとめ
参考文献・サイト
付録A: 粒子群最適化
1.はじめに
2019年末、中国湖北省武漢で発生した新型コロナ肺炎(後にCOVID-19と命名)は世界的な猛威を振い[1]、パンデミック(世界的大流行)となっています[2]。
国内でも、専門家会議[3]が立ち上がり、疫学と数理モデルの立場から施策への提言がなされました。その中で、感染症の流行において重要となる「基本再生産数:R0」「実効再生産数:RまたはRt」などの概念を、一般市民も目にすることが多くなってきました。
筆者(門)の前著「この感染は拡大か収束か:再生産数Rの物理的意味と決定」[4]において、ケルマック・マッケンドリック(Kermack–McKendrick) の「SIRモデル」として知られる最も単純な感染症の数理モデル(以下感染症モデル)で、これらの物理的意味づけと、施策、行動変容の考え方について述べました。様々な人たちが独自の評価指標や将来予測を提示する例が増えてきた一方、モデルにおける用語や評価過程に対する誤解や混乱も目にするようになってきました。
そこで、本稿では、この感染症の拡大・収束を記述する微分方程式の「意味」をより多くの方々に知っていただくことを目的に、疫学とは別の視点から感染症モデルの結果を再現してみることにしました。
微分方程式がよく使われる分野に「電子回路」があります。コイルやコンデンサは電流の時間変化(微分)に比例した電圧を発生するので、回路の方程式はまさに微分方程式です。高等学校の「物理」で学んだ方も多いでしょう。
もし、電子回路を感染症モデル(例えばSIRモデル)の微分方程式と同じ方程式を表すように実装できれば、モデルの「中身」や式の意味を気にすることなく、「一つの機能」と考え、入力と出力で感染症モデルを再現することができるでしょう。
その意味で、本稿は、電気電子系や制御工学の方々や、電気回路が好きな方々に特に親しんでいただけるように、感染症モデルと電子回路の関係について記述することを試みました。また数理モデルや疫学を専門とする方々には、別の分野からの一つの視点を提供できれば幸いに思います。
本稿「その1」では、「電子回路シミュレータ」を用いて、SIRモデルを再現することを試みました。第3章以降は、電子回路シミュレータを紹介し、簡単な例をもとに身近に感じていただくことを意図しました。回路シミュレータのソースファイルは本稿のリンクから提供しています(公開時時点)ので実際に使ってみられると、より具体的な感触がつかめると思います。
続編となる「その2」[5]では、実際の日々の新規感染者や発症者の計数データを用いて、実効再生産数Rtを求めます。
2.感染症モデルの概略 I「SIRモデル」
2-1) 本稿で扱う「感染症モデル」の概略
ここで、本稿であつかう感染症モデルの概要と注意点を述べておきます。
人口一定の「閉じた空間」(いわゆる「3密」[3]の密閉空間ではなく、人の出入りを考えないモデル上の領域のこと)、感受性人口S(Susceptible:感染する可能性のある人) 、現有感染者数I(Infectious:感染して病気になった人、あるいはSに感染させる可能性がある人)、回復数R(Recovered/Removed:回復または隔離された人)の3つ状態の人口S(t) 、 I(t)、 R(t)の時間変化を追いかけます。
前著[4]では「快復」と書きましたが、「回復」が一般的に使われてきてますので、本稿ではこちらを使います。ここでいう「隔離」とは治癒による(終生)免疫獲得または死亡であり、物理的な隔離を意味しません。[R]から[S]に戻ることを想定しないからです。ですが、短期の施策においては、隔離をあらわに含めても一般性を失いません。全人口N = S(t) + I(t) + R(t) = [一定] で、転出・転入・この感染以外による死亡は考えない、いわゆる局所モデルです。
方程式の詳細は前著[4]を参照ください。式のみ再掲すると
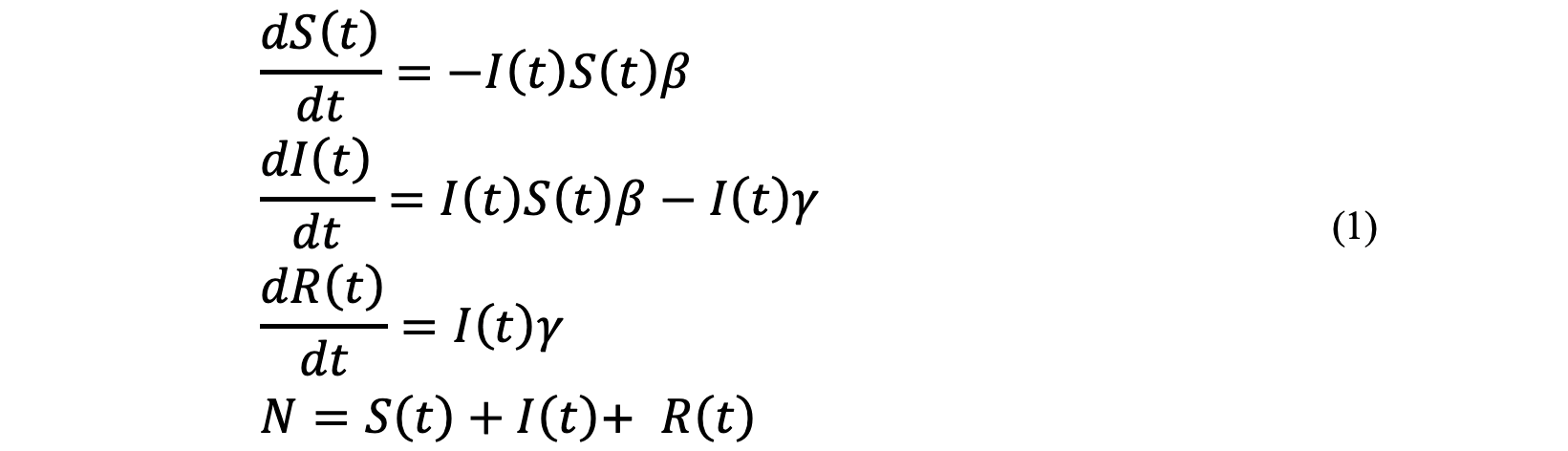
とかけます。βは感染確率(SやNと掛けたもの、すなわちSβやNβは感染の時定数の逆数)、γは回復率(時定数の逆数)です。
基本再生産数R0(アールノート; Basic reproductive/reproduction number)は、

で定義され、R0 < 1なら[I ]は指数関数で減衰するので感染は収束トレンドへ、R0 > 1 なら指数関数的(等比級数的)に感染が爆発します(感染初期なのでN = S)。時間がたって、[S]が減ったり、βが減ったりした状態は、実効再生産数(effective reproductive/reproduction number)と言われ、式(3)のように表します。記号はRやRtが用いられます。前著[4]では実効再生産数の表記にRを使いましたが、本稿では専門家会議[6]の用例にあわせ、Rtを用います。
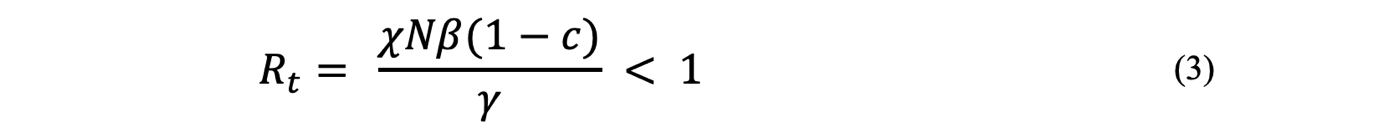
ここでc(効果率)は、各種の施策や介入、個人の防護、将来的にはワクチン接種等によって、感染確率βをどの程度減らせたか、その効果の割合を表します。つまり、βが(1-c)βに抑えられる、と解釈できます。χ = S/Nは免疫非獲得率で、χNはこれから感染する可能性がある人の数[S]そのものです。
感染の収束には、まずは実効再生産数Rt < 1を目指すことが必要条件で、さらに、医療体制の容量(surge capacity)に応じて、さらに低い値を目指します。実際、我が国の目標値は、仮定値R0 = 2.5からの8割削減が2020年4月22日に専門家会議から提言[6]されましたので、Rt < 0.5であったことがわかります。
2-2) 「単純なSIRモデル」の限界と注意点
単純なSIRモデルの限界としては
2.感染確率を表すβは様々な接触を平均化したものであり、感染機会の場面場面での強弱などは反映されないこと。
3.回復・隔離の速度(レート)を表すγは[I]が[I]でなくなる割合であり、これは実際には各集団における感染者の隔離方針などの施策に依存しないとは言えないこと(ただし、自然治癒に限ればほぼ共通と仮定するは妥当でしょう)。
4.潜伏期間、不顕性感染、免疫の喪失などは考慮されていないこと。
5.年齢差、男女差なども(とりあえずは)無視していること。
などが挙げられます。ですので、感染爆発から収束まで長期を要する新型コロナ肺炎のような感染症に対し、単純なSIRモデルを長期的な将来予測に用いる場合は、特に注意が必要です。
集団免疫獲得の判定は大きな誤解のもとであり、新型コロナ肺炎においても、集団免疫獲得を目指して死亡率が極端に増えてしまったり[7]、すでに抗体を獲得しているのでは、との憶測が出たりもしました。
前著[4]ではγとして現有感染者(発病患者)の「半減期」を用いることを提案し、中国のそれを用いました。現有感染者が一定になっている時は、日々の感染者と回復者が等しくなっているので、実効再生産数は1です。したがって、そのときのγは、実効的(仮想的)な感染者の再生産の時定数を反映していると仮定しました。その意味で、筆者(門)は「単純モデルによる」実効再生産数とことわるようにしていました。まずはこの単純モデルを電子回路シミュレータで再現してみましょう。
3.電子回路シミュレータ
3-1) LTspice
アナログ回路を扱う電子回路シミュレータはオームの法則、キルヒホッフの法則に基づき、受動素子、能動素子の物理的な特性を利用して、電圧、電流の過渡現象、周波数応答など様々な現象を演算することができます。ここで「応答」という言葉は、ある機能を持つ「箱(ブラックボックス)」に入力と出力があるとして、入力に対して、どんな出力が得られるか、これをその「箱」の「応答」と呼びます。周波数応答とは、入力信号の周波数特性が出力信号でどう変わるかという「応答」です。
本稿では、SPICE(Simulation Program with Integrated Circuit Emphasis)という1973年にカリフォルニア大学バークレー校で開発されたソフトウエアから派生し、アナログ・デバイセズ社(旧リニアテクノロジー社)で開発されたLTspice [8]というソフトウエア を使用します。2020年6月現在のバージョンはWindows 7、8、10用LTspice XVII、Mac OS X10.7+用LTspice XVII for OS Xです。
SPICEの仕組みを簡単に説明すると、ネットリストと呼ばれる各素子の結線情報と、部品の電気的特性データをもつモデル・ライブラリをもとに、電子回路を行列(=回路方程式)に変換し、各種の演算を行います。
受動素子のインダクタ(コイル)やキャパシタ(コンデンサ)のような微分、積分にあたる演算も数値積分法により実現します。LTspiceはスイッチング・レギュレータ回路(電子素子だけで電圧を変換する変圧器の回路)のシミュレーションを目的に作られており、数値積分をする際にスイッチング波形のような急峻な変化を捉えられるよう工夫がなされています。
筆者(神田)が考えるLTspiceの利点は
- 無料で扱えること、
- 部品やノード数に制限がないこと、
- 使用にあたり難しい設定を必要としない
などが挙げられます。
3-2) アナログコンピュータ
アナログ電子回路シミュレータが微分項を含んだ回路方程式(すなわち微分方程式)を過渡解析する場合は、数値解析にて演算を行います。インダクタやキャパシタのような微分要素が混ざった微分方程式の場合は、数値積分演算を行います。
まだ今日のようにディジタルコンピュータが発達していなかった頃、物理現象を用いて微分方程式を解く計算機がありました。これは、アナログコンピュータ[9]や微分解析機などと呼ばれていました。
本稿で扱うのは電気信号で演算を行う、いわば電子式のアナログコンピュータです。
アナログという連続量を用いた計算機の歴史は古く、有名なところでアンティキティラ島の歯車があります。これは天体の動きを複数の歯車を用いて模擬したアナログ計算機と考えられています。実は、LTspice(Windows用LTspice XVII)を起動したときに現れる背景画像は、その歯車のイラストになっているのです(図1(a))。
 図1.(a) Windows用LTspiceの起動後の画面。デフォルトの背景はアンティキティラ島の歯車。 (b)円型の計算尺。
図1.(a) Windows用LTspiceの起動後の画面。デフォルトの背景はアンティキティラ島の歯車。 (b)円型の計算尺。ジョン・ネイピア(John Napier)が1614年に対数の概念を考案し、1632年にウィリアム・オートレッド(William Oughtred)が固定尺と滑尺とよばれる2つの定規に対数の目盛を割り当てることで、乗算除算を可能にした計算尺が発明されました。図1 (b) は円型の計算尺で、現在でも購入できる計算尺のひとつです。円型計算尺の場合、角度という連続量に対し、乗算除算、平方根や三角関数など割り当てることで計算を実現しています。
微分方程式を解くことができる微分解析機と呼ばれる機械式アナログコンピュータが発明されたのが1876年で、実用的な計算機は1928年から1931年にかけてマサチューセッツ工科大学のヴァネヴァー・ブッシュ(Vannevar Bush)らにより開発されました。このブッシュ式微分解析機は東京理科大学の近代科学資料館にて動態保存されており、日本国内で唯一現存する微分解析機です(2020年6月現在ではリニューアルのため休館中)[10] 。ちなみにディジタル回路を生み出したクロード・シャノン(Claude Elwood Shannon)はブッシュの教え子でした。
アナログコンピュータの構成要素として必要だったのが高い入力インピーダンス、高いゲインの増幅回路です。これが今日に伝わるオペアンプ(演算増幅器)の原型になっています。数値演算としてはほとんどディジタルコンピュータに取って代わられてしまい、かつてのようなアナログ回路で行うことはほぼなくなってしまいました。しかしアナログコンピュータは信号増幅や周波数フィルタ処理、フィードバック制御など、形を変えて使われ続けています。
3-3) アナログコンピュータの構成要素[11]
アナログコンピュータで微分方程式を解くための構成要素を図2に示します。
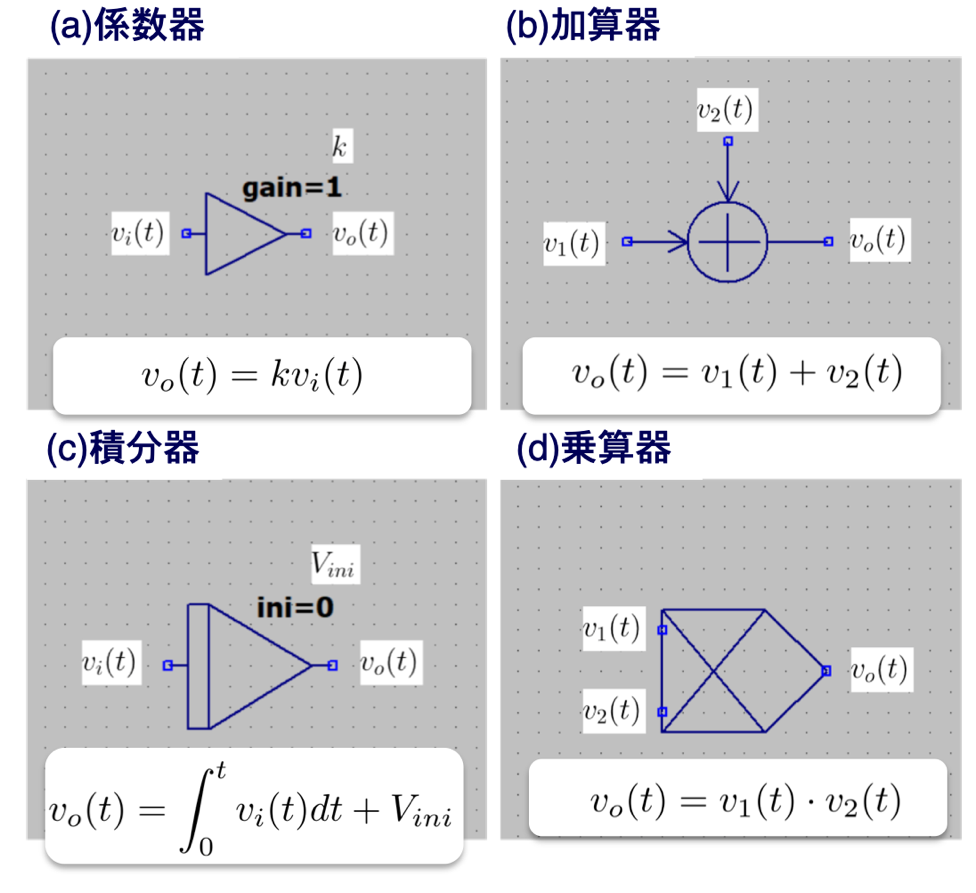 図2. (a)係数器。入力された電圧に対し、定数倍する回路。(b)加算器
図2. (a)係数器。入力された電圧に対し、定数倍する回路。(b)加算器2つ以上の電圧の加算値を出力する。(c)積分器。入力された電圧に対し、時間積分した電圧を出力する。(d)乗算器。2つの入力電圧に対して乗算する
簡単な微分方程式を解くだけであれば図2(a)〜(c)の係数器、加算器、積分器の3つの要素で十分ですが、本稿ではそれに加え、図2(d)の乗算器を用います。
4.簡単な例 〜運動方程式を解く〜
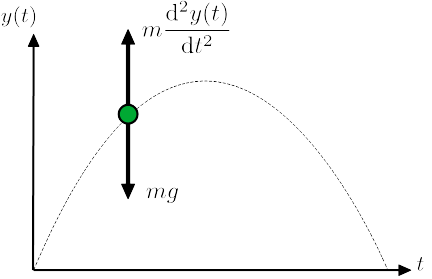 図3.ボールの投げ上げ運動のy-t グラフ。横軸方向は時間t。y方向は高さ。
図3.ボールの投げ上げ運動のy-t グラフ。横軸方向は時間t。y方向は高さ。
まずは「小手調べ」に、図3に示すボールの鉛直投射をシミュレーションしてみましょう。ニュートンの運動方程式F=ma(m:質量、a:加速度)に当てはめると、gを重力加速度(=9.8 m/s2 )として

と書けることは高等学校の物理基礎で学びます(ね?)。両辺をmで割り、加速度は位置座標yの2階微分であることを考慮すると、

です。これをアナログコンピュータで解くには図4に示す手順に従います。
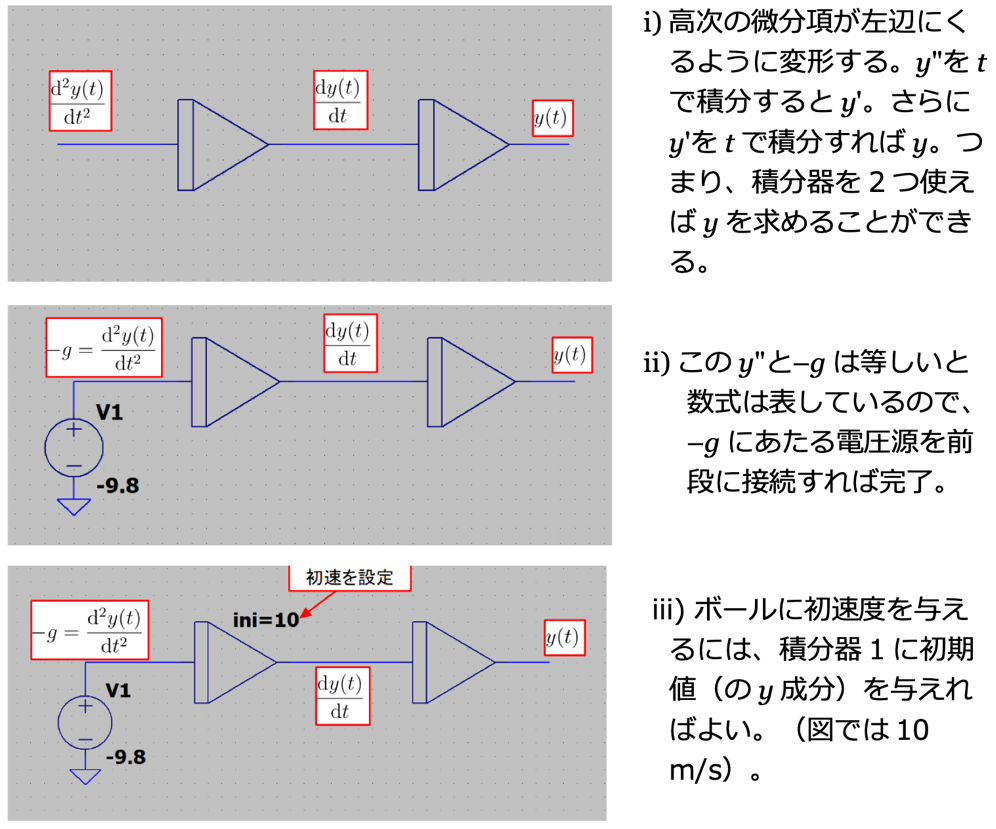 図4.運動方程式の実装手順。
図4.運動方程式の実装手順。時刻3秒までシミュレーションをおこなってみます(過渡解析)。例えば高さ1 mを電圧1 Vとして直読するようにします(好きに作れます)。設定画面を図5に示します
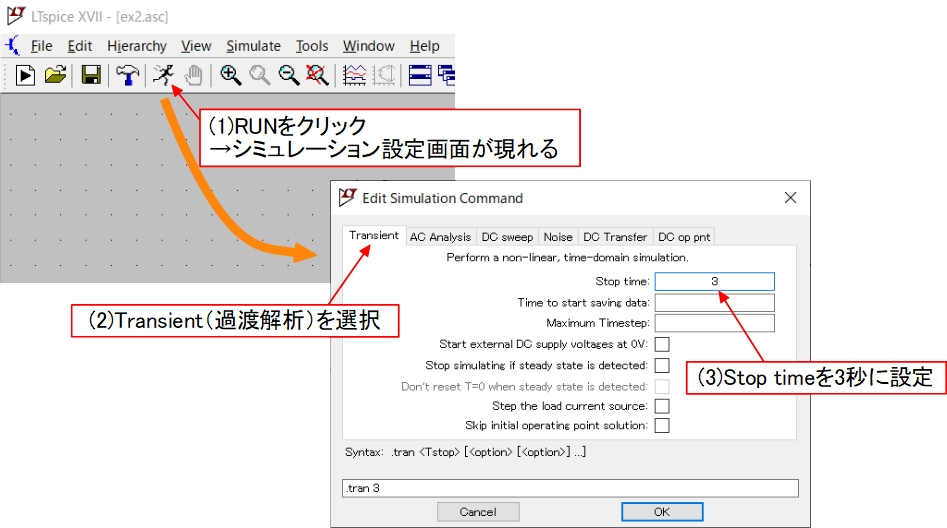 図5.本章の運動方程式を解くためのLTspice(Windows用)の設定例。Mac用は設定画面への入る操作が若干異なる。
図5.本章の運動方程式を解くためのLTspice(Windows用)の設定例。Mac用は設定画面への入る操作が若干異なる。結果を図6に示します。横軸は時間[秒]、縦軸は電圧(すなわち高さ)です。このようにグラフ表示もソフトウエアがやってくれます。さらに、この出力の数値データをファイル出力し、別のソフトウエアで解析することも可能です。
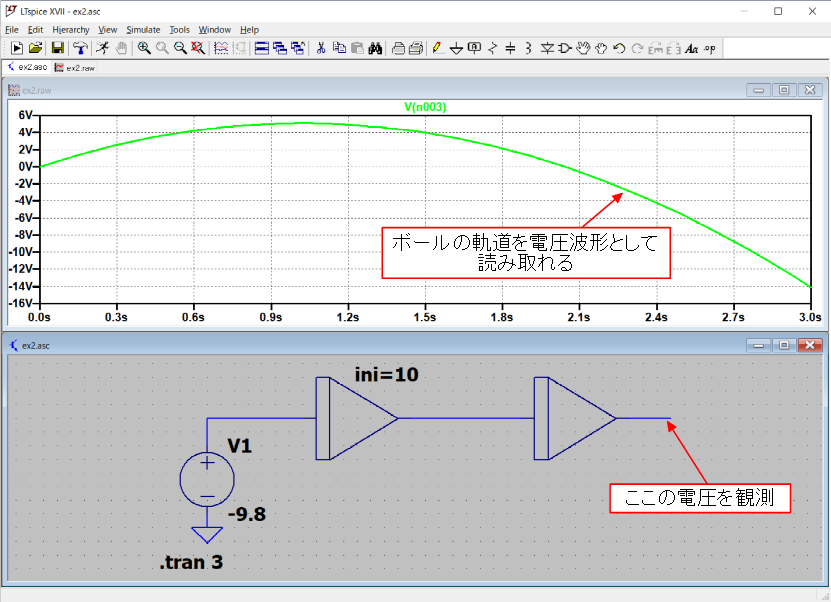 図6.演算結果。ボールの軌道を電圧波形として読み取れる。
図6.演算結果。ボールの軌道を電圧波形として読み取れる。いかがでしょうか。簡単な回路構成で、しかも一度回路を作ってしまえば、初期値をその場で変えるだけでシミュレーションできる、専用のコンピュータとなるのです。
5.SIRモデルへの適用
5-1) 物理量との対応条件の設定
前項の手順にしたがって、SIRモデルの回路シミュレータへの実装をしてみましょう。電圧1 V を1人と割り当て、シミュレーション時間1秒を現実の1日に割り当てます。東洋経済オンライン[12] より発表されている新型コロナ感染症のデータをもとに、S(t)、I(t)、R(t)を物理量と対応させ、初期値を設定しました。
I(t) : 現有の感染者数(人に感染させる可能性のある人)
R(t) : 除去者 = 退院者+人工呼吸器又は集中治療室に入院している者+死亡者
S(0) = 1億人 (=100 MV ) 日本のおおよその総人口
I(0) = 16人 (=16 V ) 2020年2月6日時点のPCR検査陽性者の累計値
R(0) = 0人 除去者の初期値
5-2) S(t)を解くアナログコンピュータの構築
前章と同様に、アナログコンピュータを構築しましょう。連立微分方程式なので、複数の方程式を接続することになりますが、まずは1つ目の方程式の作り方を図7に順を追って示します。
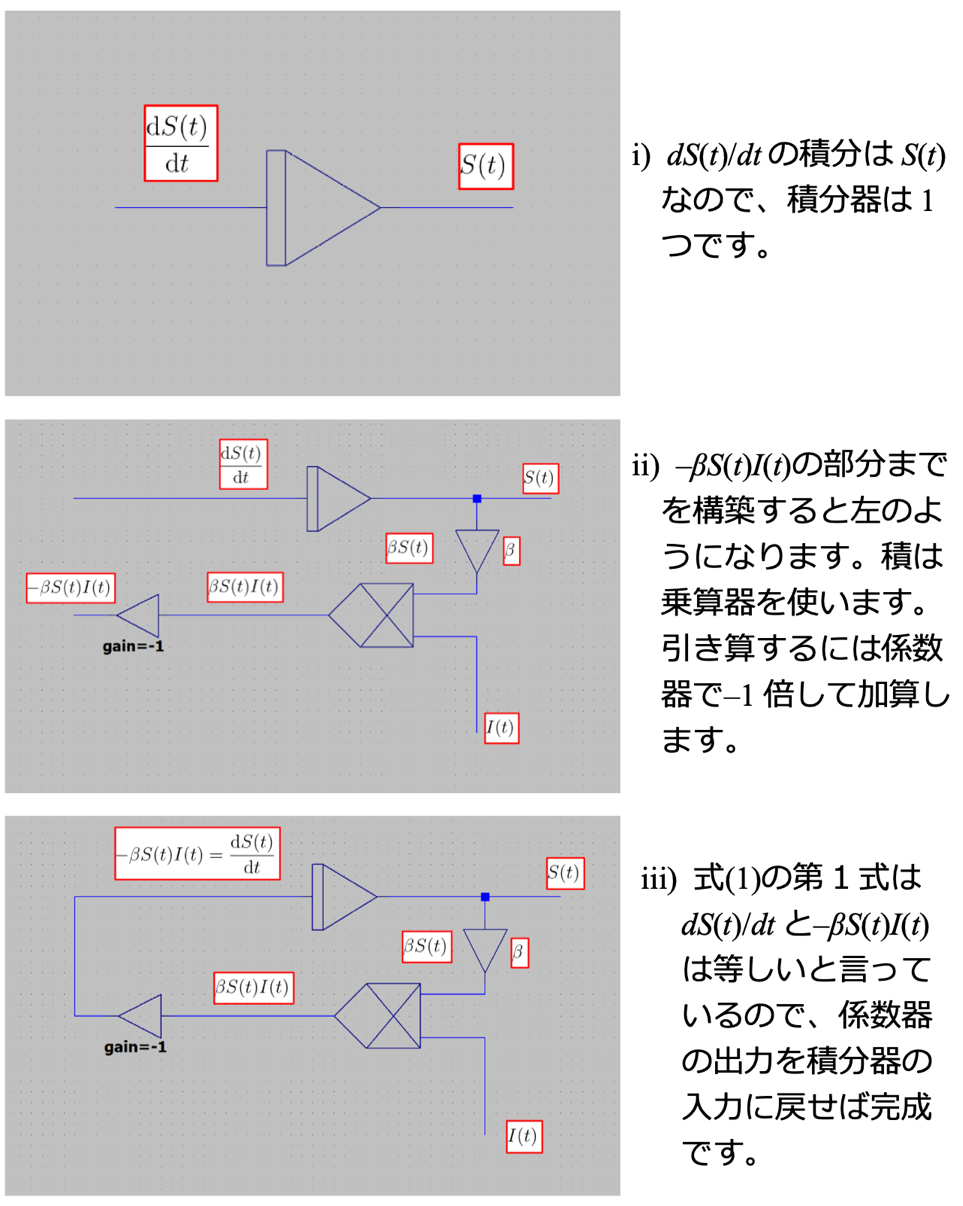 図7.SIRモデルを演算するアナログコンピュータの構築手順
図7.SIRモデルを演算するアナログコンピュータの構築手順残りのI(t)、R(t)の部分も構築して、和には加算器をつかって、図8のようにお互いを接続します。
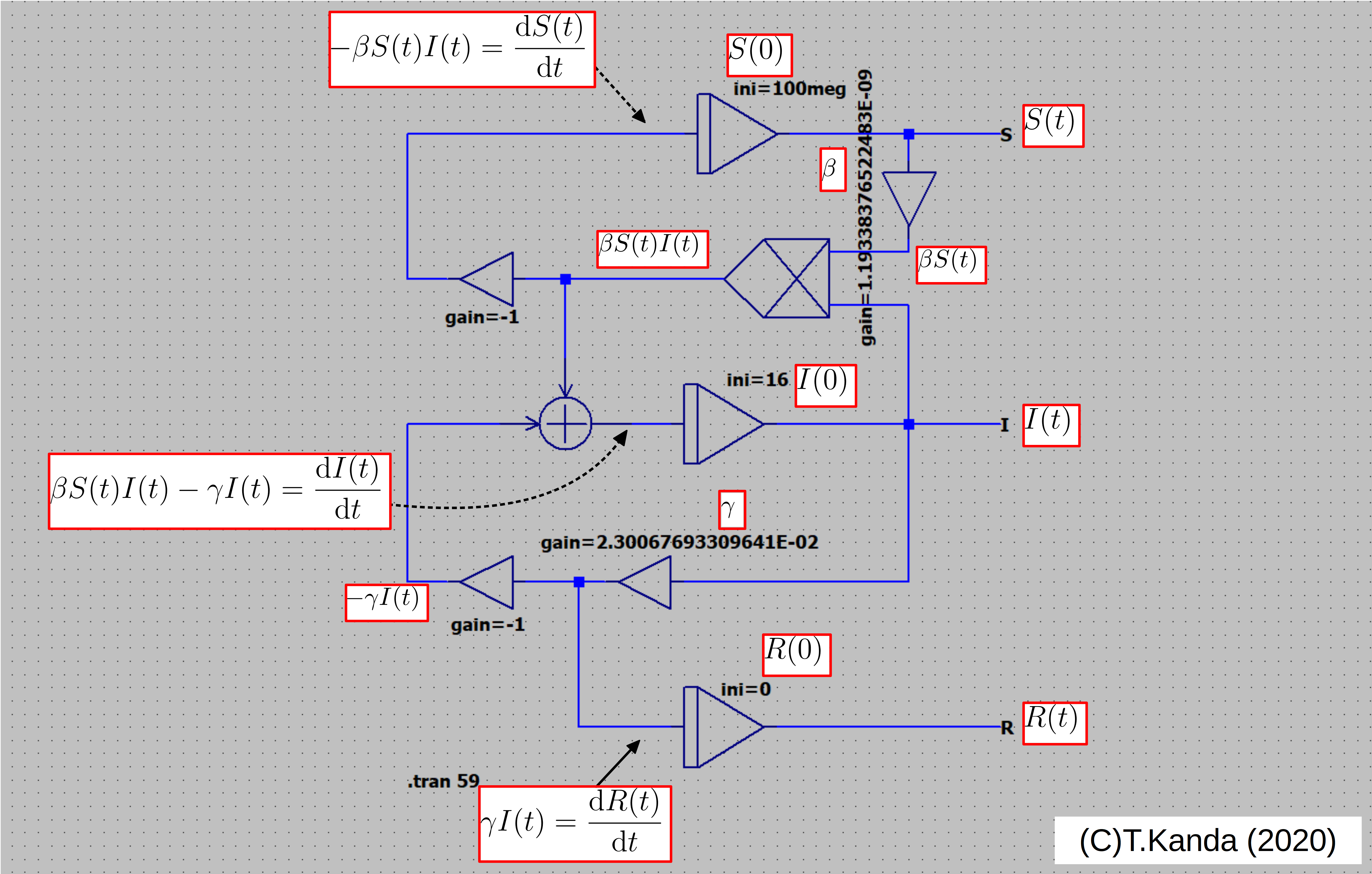 図8.SIRモデルを演算するアナログコンピュータ完成図
図8.SIRモデルを演算するアナログコンピュータ完成図いよいよ、計算に移ります。βとγは東洋経済オンライン[12] より発表されているデータの2020年2月6日~2020年4月7日のデータを基に決定しました。決定には、付録Aに示した「粒子群最適化」という手法を用いました。実測値に合うような複数の変数の組み合わせを探索する一つの方法です。決定した値を以下に示します。
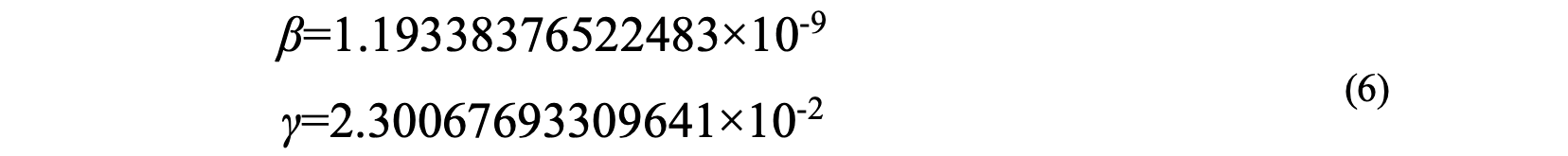
(桁は有効桁数を気にせず目一杯示しています。)
少し注意いただきたいのは、少ないデータからβとγを同時に決定する場合は、両者のバランスで最適値を探すので、両者の現実の物理量を反映するとは限らない点です。
求めたβとγを用いて解いたSIRモデルの解(S、I、Rの時間変化)を図9に示します。
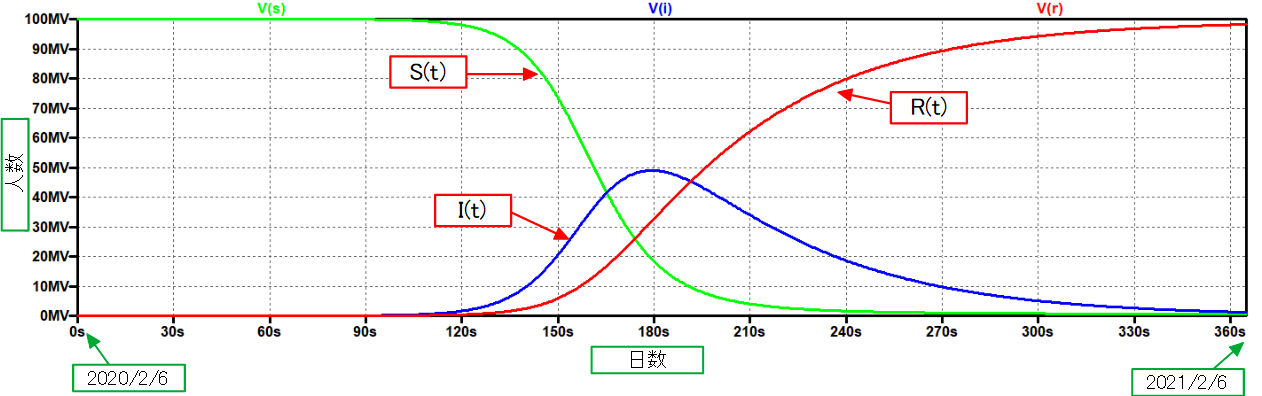 図9.アナログコンピュータによるSIRモデルの計算結果
図9.アナログコンピュータによるSIRモデルの計算結果いかがでしょうか。全貌がみえてきたのではないでしょうか。SIRモデルによる計算でよく見かける図を再現することができました。これをもとに、いろいろな状況を想定した計算が可能です。
5-3)行動変容の組み込み
感染拡大防止のために、専門家会議が2020年3月19日に提唱した「行動変容」[6]は、ある時刻以降、接触機会×感染確率 (Sβ)をSβ (1-c)に低減することを意味します[4]。cは式(3)で述べた効果率(efficacy)で、自粛、マスク、ソーシャルディスタンシング(いわゆる3密(密閉・密集・密接)を避ける)などの予防措置、あるいはワクチン接種、都市封鎖(ロックダウン)などの介入を含めた総合的な値です。
効果率cを与えるには、図10のように係数器βのあとに(1-c)を乗ずる回路を設けます(Sはそのままにして、効果をβに帰着させていることになります)。係数器で直接定数を与えてもよいのですが、LTspiceには任意の定数を変化させることができる「step」という命令がありますので、乗算器を用いて与えます。具体的には、ある時刻から1-cを乗じたいので、電圧源V2から任意の波形を与えられるようにします。
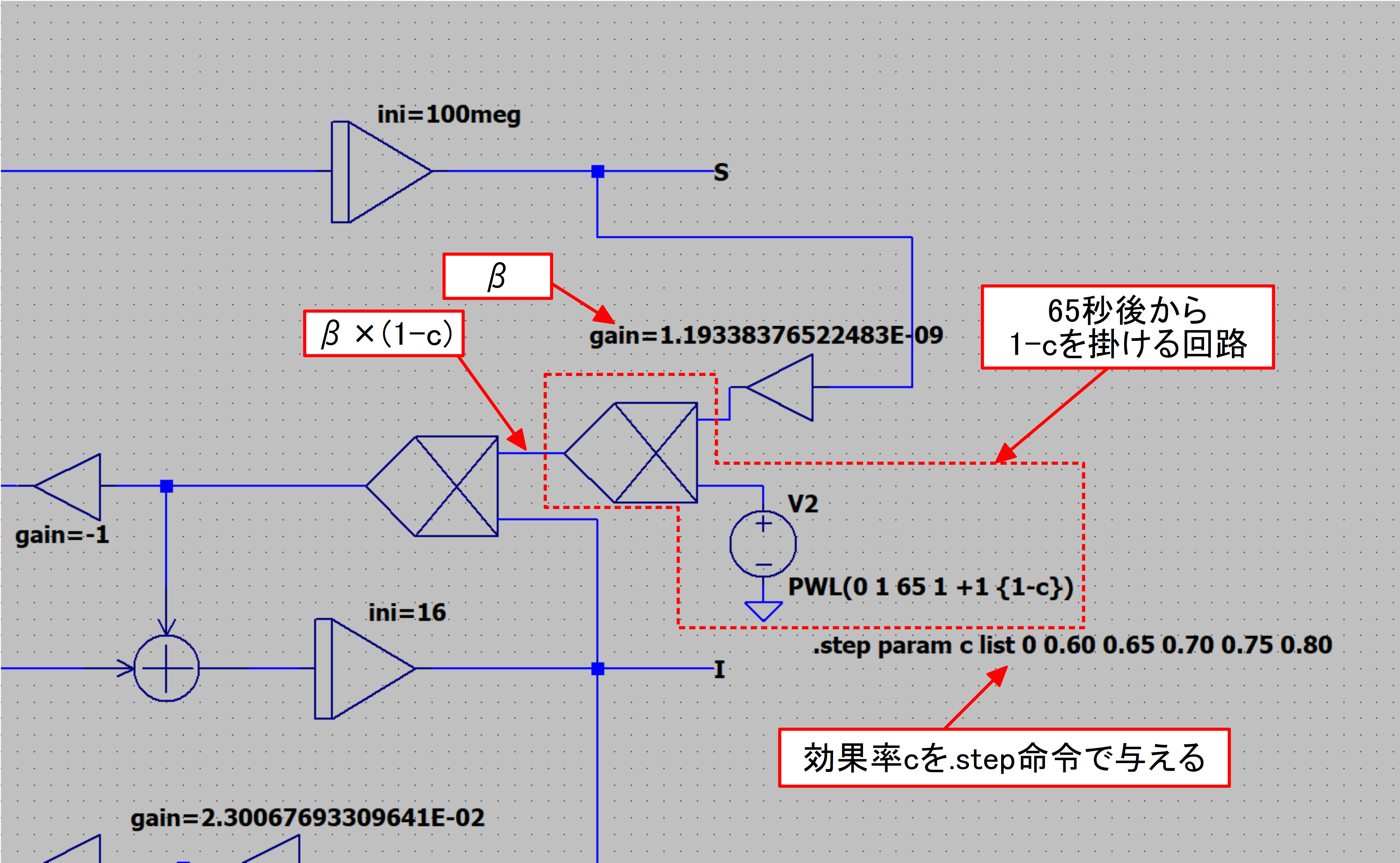 図10.効果率cを考慮し、(1-c) を乗ずる回路(赤点線の囲み部分)を追加
図10.効果率cを考慮し、(1-c) を乗ずる回路(赤点線の囲み部分)を追加結果を図11に示します。行動変容によって、ピークを下げ、長丁場(長期戦)にもつれ込んでいく様子が再現できていると思います(この戦略で体制を整え、医療崩壊を防ぎます[4])。
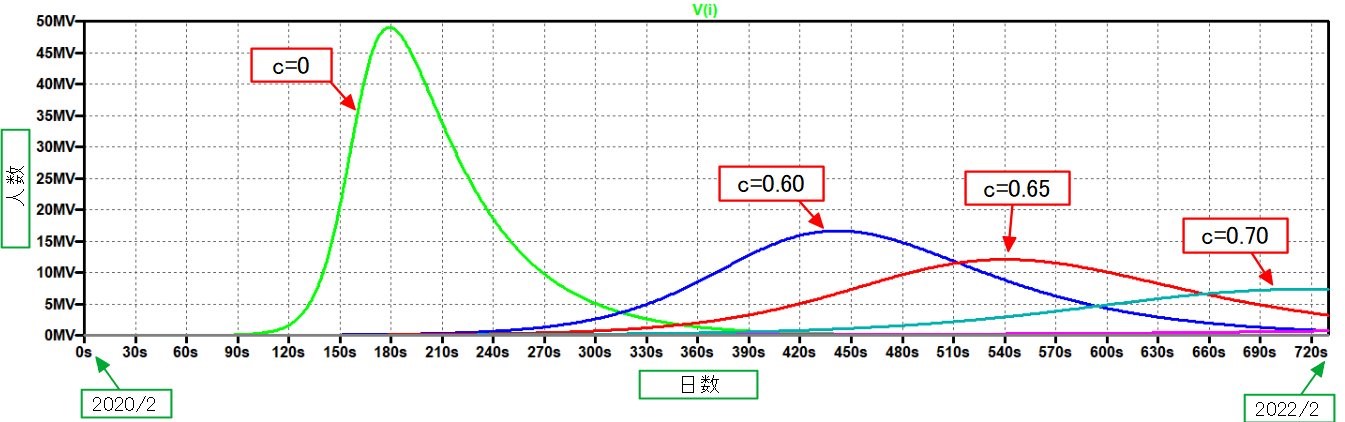 図11.自粛などの行動変容によってβ → β(1-c)としたときの現有感染者数[I]の経時変化。60%削減(c=0.60)、65%削減(c=0.65)、70%削減(c=0.70)によって現れる効果の違いがわかる。
図11.自粛などの行動変容によってβ → β(1-c)としたときの現有感染者数[I]の経時変化。60%削減(c=0.60)、65%削減(c=0.65)、70%削減(c=0.70)によって現れる効果の違いがわかる。電圧源には任意の波形を与えられるので、図11のように自粛をし続けるのではなく、一定期間のみ c ある時刻以降の効果を入れることも可能です。
例えば緊急事態宣言やロックダウンなどの行動の自粛要請は一定期間のみであり、解除された場合は元の行動にもどると考えられます。このように一定期間だけ自粛するとどうなるかをみてみましょう。
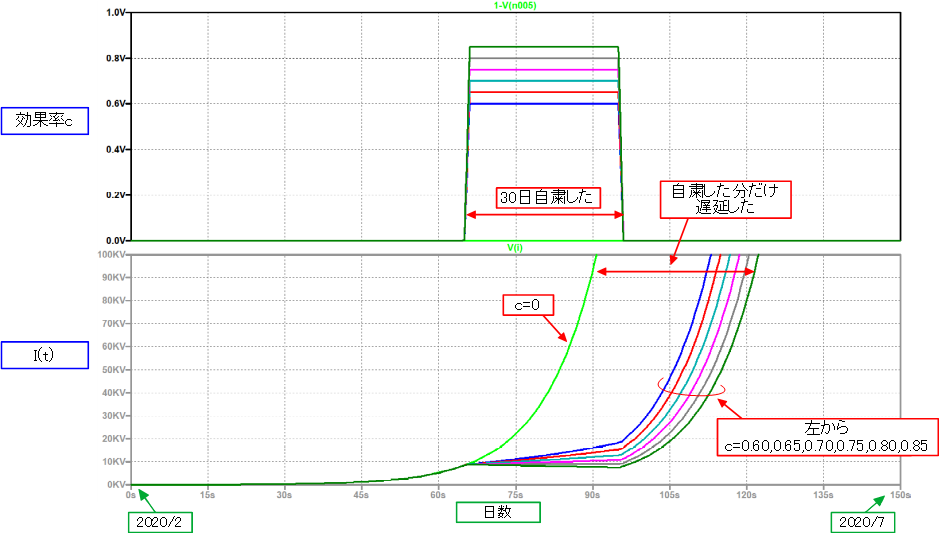 図12.一定期間のみ効果率cを乗じた場合の現有感染者[I]の経時変化
図12.一定期間のみ効果率cを乗じた場合の現有感染者[I]の経時変化図12に効果率cの時間波形、およびそのcを用いた場合の現有感染者[I]の動向を示します。「人との接触機会を8割減らす」[6]とは、cの値が0.8となるように防護策をとり、結果、感染率を20%に抑えることを意味します。γの値は固定ですので、実効再生産数を5分の1にしよう、とする目標設定とも言えます。
6.「その1」まとめ
繰り返しになりますが、重要なことは、本稿にシミュレーションしたSIRモデルは、日々や場所によって大きくかわる接触機会や隔離率をすべて一定としますので、将来予測には使えません。集団免疫獲得の予測に使うのはとりわけ危険でもあります。さらに、実効再生産数としていくつを目標に設定するかは、地域の医療体制の容量にも大きく依存することを忘れてはいけません。あくまで、行動変容の指針や評価を検討する際の一つのツールとして扱うのが適切に思います。
とはいえ、このような演習的なシミュレーションを通じて、少しでも多くの方々に感染症の数理モデルの「見方」「考え方」を知ってもらうことは、専門家会議による提言や政府の施策をより正しく判断する有用なリテラシーを与えるものであると信じます。
「その2」[5] では、より実用的な観点から実効再生産数Rtを電子回路シミュレータで求める手法を紹介します。実際に公表されている日々の感染者数のデータに適用することが可能です。
(その2[5]へ続く)
[1] アメリカCDC、COVID-19のページ:https://www.cdc.gov/coronavirus/2019-nCoV/index.html (2020年6月22日閲覧) [2] “WHO Director-General’s opening remarks at the media briefing on COVID-19 – 11 March 2020”, https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19—11-march-2020 (2020年6月22日閲覧) [3] 新型コロナウイルス感染症対策専門家会議: https://ja.wikipedia.org/wiki/新型コロナウイルス感染症対策専門家会議 (2020年6月22日閲覧) [4] 門 信一郎:この感染は拡大か収束か:再生産数Rの物理的意味と決定, RAD-IT21 WEBマガジン (2020.03.27) https://rad-it21.com/サイエンス/kado-shinichiro_20200327/ [5] 門 信一郎、神田 峻彦:電子回路シミュレータで解く感染症モデル「その2〜実効再生産数を求めよう〜」, RAD-IT21 WEBマガジン (2020.07.14) , https://rad-it21.com/サイエンス/kado_kanda_20200714_2/ [6]「新型コロナウイルス感染症対策の状況分析・提言」(2020年4月22日)https://www.mhlw.go.jp/stf/seisakunitsuite/bunya/0000121431_00093.html [7] BBCニュース – 【解説】 なぜイギリスは方向転換したのか 新型ウイルス対策 https://www.bbc.com/japanese/features-and-analysis-51996098 (2020年6月22日閲覧) [8] アナログ・デバイセズ社。LTspiceダウンロードサイト。https://www.analog.com/jp/design-center/design-tools-and-calculators/ltspice-simulator.html# [9] アナログ計算機, Wikipedia, http://ja.wikipedia.org/wiki/アナログ計算機, (2020年6月22日閲覧) [10] 東京理科大学近代科学資料館, https://www.tus.ac.jp/info/setubi/museum/ , (2020年6月22日閲覧) [11] 黒川一夫, 現代講座アナログ・ハイブリッド計算機, 1969年, オーム社. [12] 東洋経済オンライン特設ページ(新型コロナウイルス国内感染の状況)https://toyokeizai.net/sp/visual/tko/covid19/ (2020年6月22日閲覧)
粒子群最適化[A1]はParticle Swarm Optimizationの頭文字をとってPSOとも呼ばれています。これは鳥や魚の群れが群れの中で情報を共有しあい、もっとも良い餌場を探す様子を模擬したメタヒューリスティクスアルゴリズム(組み合わせ最適化問題における発見法的な解決手法)のひとつです。
もう少し噛み砕いて説明すると、「ある値とある値の間が良さそうだから、中間の値ぐらいの定数で試してみよう」とやりながら回路の調整をしている行為を行っているといえばイメージがつきやすいかと思います。求めたい数値の組み合わせというのを粒子の座標という形で表し、複数個の粒子を式(A1)、式(A2)の制御式に従って変化させ、最適解を見つける手法になります。
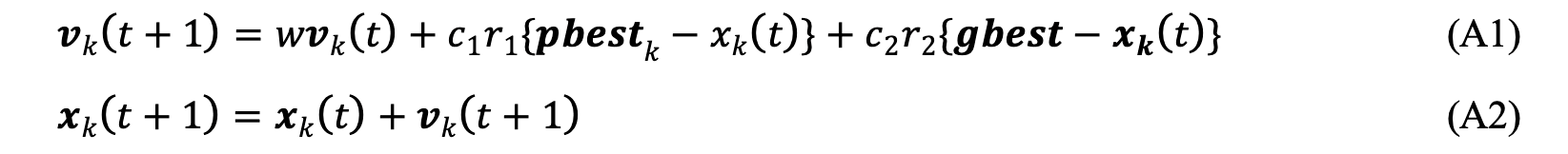
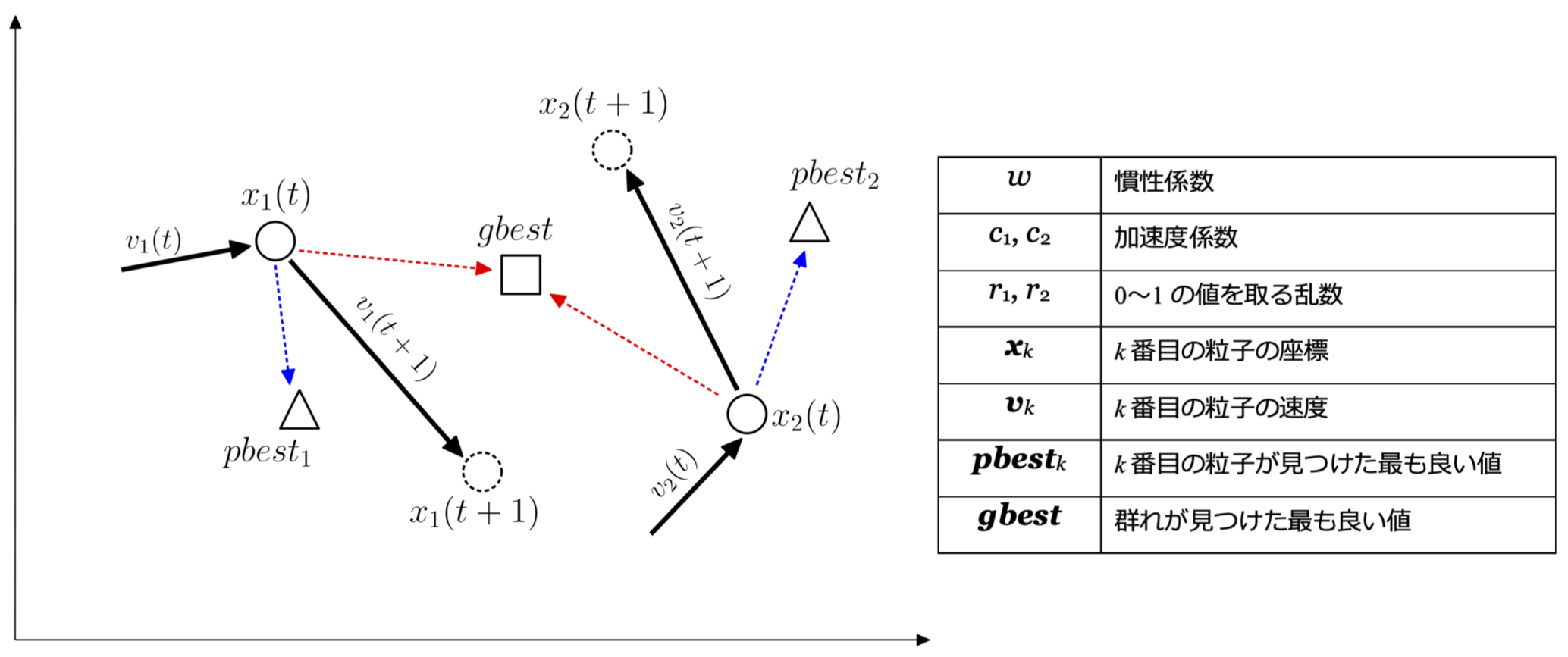 図A.粒子群最適化(PSO)の概念図
図A.粒子群最適化(PSO)の概念図図Aに2つの粒子が最適解を探し回る様子を表します。
x、v、 pbest、 gbestをベクトルで書いたのは、求めたい数値が複数個ある=多次元空間の座標のことを意味しています。数値がa ~ eの5つある場合、たとえばxはx = (a, b, c, d, e)のようになります。粒子の数には制限はありませんが、たくさんあったほうが探索範囲をまんべんなく探索できます。
k番目の粒子はxという座標情報、vという速度情報、今まで探索してきて最も良い値pbest を持っています。また、すべての粒子のpbestを集約し、群れの中で最も良い値gbestを決定します。
ある時刻tにおいて、式(A1)にしたがって速度を決定し、式(A2)で次に探索する座標を決定します。この速度vは次の組み合わせの数値を決定するための変化させる量になりますが、最適解に近づいてくると、この変化量は減っていき、やがてゼロに収束していきます。
自動的に最適値を探索していくアルゴリズムもありますが、本稿の解析の場合は各素子の値を座標に割り当てて、手動で変数を変えていきながら、目標のβ、γ(本稿「その1」式(6))や伝達関数(本稿「その2」の式(3))に近くなるような組み合わせを探しました。
[A1] 粒子群最適化法, https://www.msi.co.jp/s4/introduction/pso.html, (参照 2020-04-23)